검색결과 리스트
공대생의 팁에 해당되는 글 122건
- 2021.08.01 VMware에 안드로이드 설치 도중 부팅이 멈출 때 해결방법 4
- 2021.06.11 PowerShell을 사용하여 폴더 내의 파일명을 한 번에 바꾸기
- 2021.05.16 VMware에서 Fedora에 VMware Tools 설치 후에도 해상도 변경이 안될때
- 2021.04.30 Windows Powershell 명령어를 바로가기로 구현하기 1
- 2021.03.23 부팅시 grub가 화면에 나오지는 않으나 정상적으로 동작할 때 해결방법
- 2021.03.16 python에서 pip install 과정에서 SSL 오류 해결방법
- 2021.03.11 USB없이 GRUB2를 통해 ISO파일 부팅하기(DVD 없이 우분투 설치)
- 2021.02.01 Gower's distance(가워 거리) 2
- 2021.01.16 2021년 이후 어도비 플래시 플레이어를 사용하는 방법 4
- 2020.10.25 MobaXterm에서 X server 사용시 전체화면 모드 화면이 안나올때 해결방법 1
- 2020.09.13 여분기여도(Marginal Contribution)
- 2020.09.12 Chernoff bound(체르노프 유계)
글
VMware에 안드로이드 설치 도중 부팅이 멈출 때 해결방법
이전에 안드로이드 x86을 VirtualBox를 통해 설치하던 도중 부팅 화면이 나오지 않았던 경험이 있었습니다. 그 당시엔 그래픽카드 설정을 통해 해결하였던 적이 있었지요.
VirtualBox에 안드로이드 설치 도중 부팅이 멈출 때 해결방법
한동안 안드로이드와는 거리를 두고 지내던 도중 종종 관련 질문이 들어와서 최신 버전인 Oreo를 VirtualBox에 설치를 아래와 같은 방식으로 시도해 보았었습니다. 안드로이드 버추얼박스(VirtualBox
elecs.tistory.com
이번에도 안드로이드 운영체제에서 테스트해보고자 하던 기능이 있어서 이번에는 VMware Player에서 안드로이드 x86을 설치해보았는데 이번에도 부팅이 멈추는 현상이 나타납니다.
x86_64:/ #
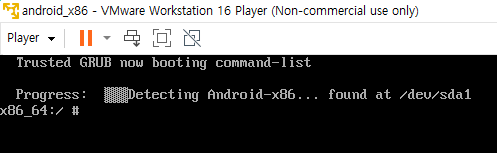
VMware Player의 경우 설정에 제약이 있기 때문에 이를 해결하기 위해서는 부팅 과정에서의 설정 자체를 바꿔야 할 것으로 보입니다. 일단 안드로이드 x86 설치시 grub를 필수로 설치해주신 후 아래의 화면과 같이 Debug Mode로 접근합니다.
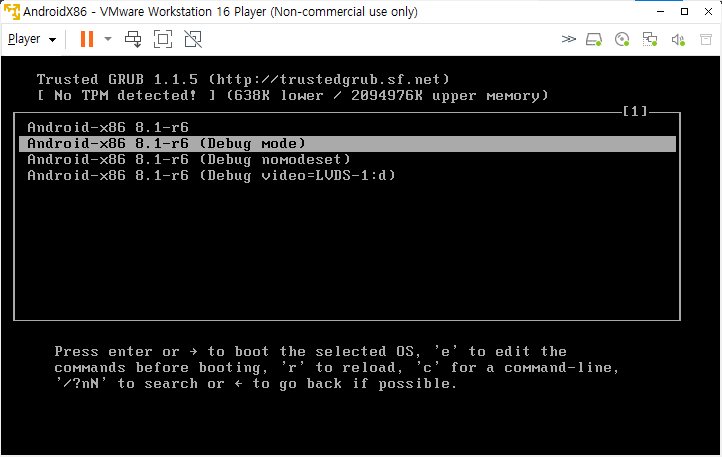
Debug mode에 진입하면 온갖 문자들이 쏟아지는 화면을 볼 수 있습니다. 문자들이 모두 지나간 것으로 보이면 엔터를 연타하여 명령어를 칠 수 있는 화면이 보이게 해줍니다.
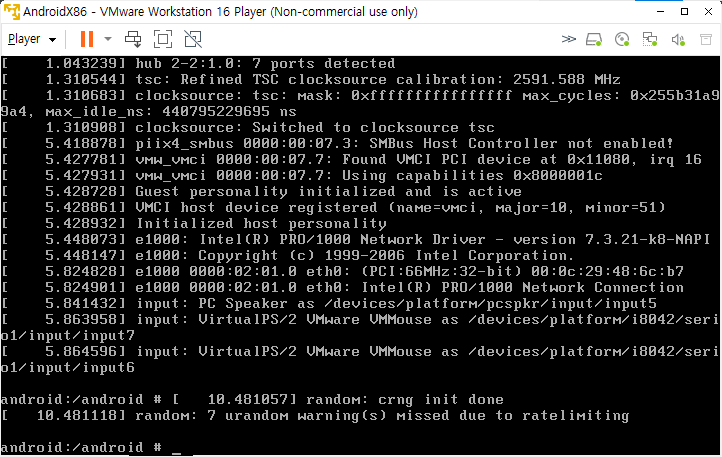
다음과 같이 입력하여 grub 메뉴를 수정해줍니다.
# mount -o remount,rw /mnt
# vi /mnt/grub/menu.lst
이제 아래와 같은 내용이 나오면 첫번째 줄 'title Android-x86 ~~' 부분에서 kernel /android ~ 줄에서 quiet를 지워주시고 다음과 같은 내용을 적어주세요.
vi에서 텍스트를 수정하기 위해 'i' 버튼을 눌러주세요.
quietnomodeset xforcevesa
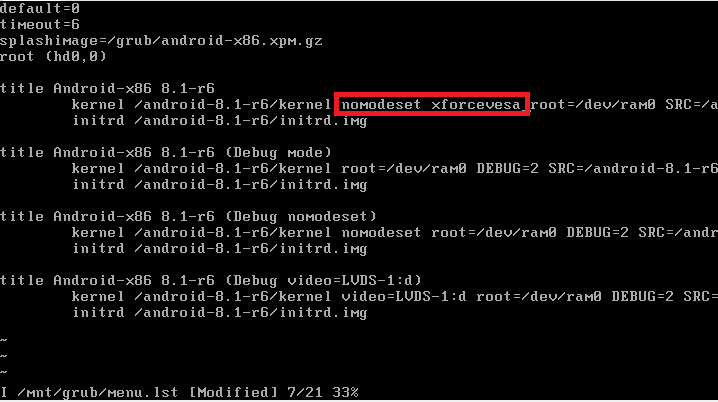
수정이 완료되었다면 해당 모드에서 빠져나오기 위해 Esc 버튼을 누르신 후 vi 내용을 저장하고 빠져나옵니다.
:wq
이제 Debug 모드를 빠져나와 리셋을 한 다음 수정된 grub 내용을 실행시키면 아래와 같이 정상적으로 부팅됨을 확인하실 수 있습니다.
# reboot -f

'공대생의 팁' 카테고리의 다른 글
| Linux에 USIM을 꽂아 통신사 데이터를 써보자! 우분투에서 LTE USB 모뎀 사용방법 (0) | 2021.08.21 |
|---|---|
| Fedora 패키지 저장소 dnf 속도 빠른 서버 자동 설정 방법 (0) | 2021.08.11 |
| PowerShell을 사용하여 폴더 내의 파일명을 한 번에 바꾸기 (0) | 2021.06.11 |
| VMware에서 Fedora에 VMware Tools 설치 후에도 해상도 변경이 안될때 (0) | 2021.05.16 |
| Windows Powershell 명령어를 바로가기로 구현하기 (1) | 2021.04.30 |
설정
트랙백
댓글
글
PowerShell을 사용하여 폴더 내의 파일명을 한 번에 바꾸기
우분투에서 터미널을 다룰 때 다량의 파일들을 처리할 때 간단한 명령어로 쉽게 처리하곤 했었습니다. Windows에서도 많은 양의 파일을 다루게 되었을 때 우분투에서는 쉽게 생각해낼 수 있는 명령어가 익숙치 않아 찾아보던 도중 괜찮은 내용이 있어 이렇게 여러분들께 공유해보고자 합니다.
Windows를 사용함에 있어 가장 큰 장점은 사용하기 쉬운 UI를 통해 사용자가 편하게 애플리케이션을 제어할 수 있다는 점입니다. 특히 파일명을 바꾸고 싶을 때는 아래와 같이 파일 이름을 한 번 사뿐이 클릭만 해주면 바로 바꿀 수 있게 되어 있다는 것이지요.
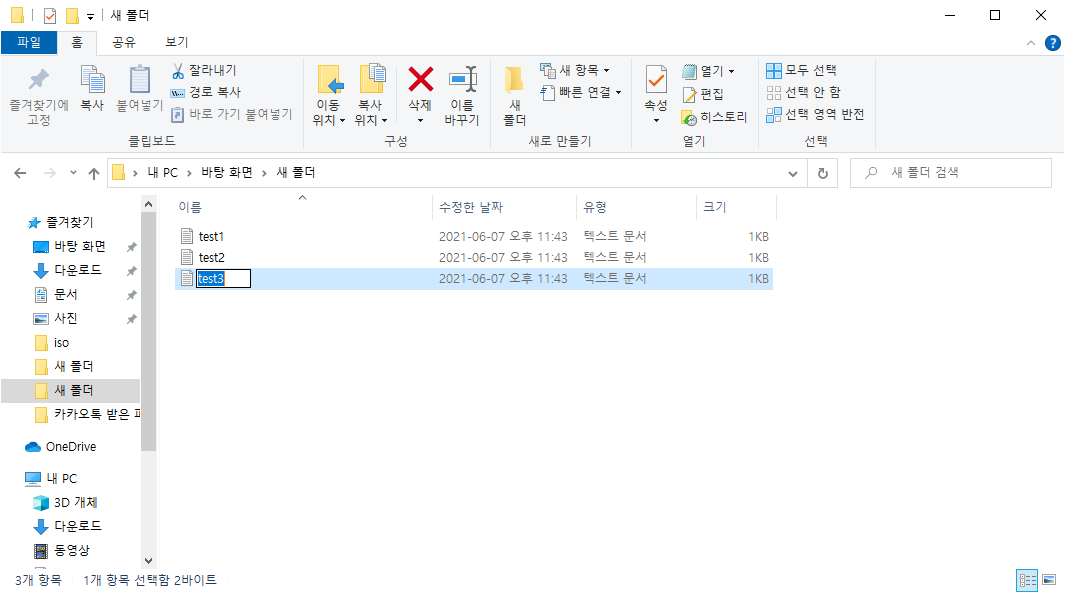
그러나 아무리 사용이 편한 Windows라고 할지라도 파일의 갯수가 수천개 이상일 경우 이러한 방식으로 일일히 파일명을 변경하려 하는 것은 상당한 시간 낭비입니다. 그렇다면 Windows에서도 우분투의 터미널처렴 간단한 명령어로 파일명을 변경하는 방법은 없을까요?
Windows에서도 강력한 CLI 환경인 PowerShell을 제공합니다. 이름 변경을 원하는 폴더 화면에서 Shift+오른쪽마우스버튼을 클릭하면 아래와 같이 '여기에 PowerShell 창 열기'라는 메뉴가 나타납니다. 해당 메뉴를 클릭해줍니다.
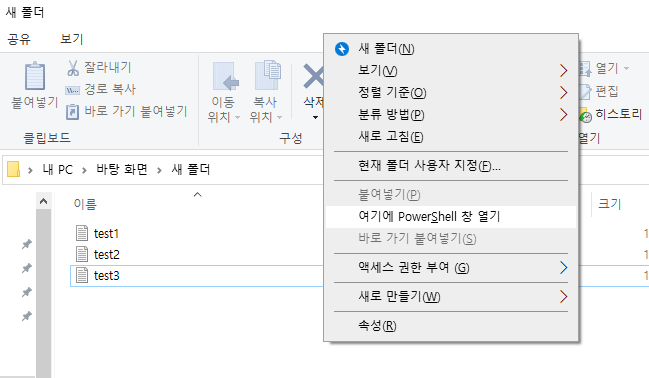
이 과정을 거치면 여러분의 컴퓨터 환경에서 PowerShell을 사용할 수 있게 됩니다.
만약 여러분들이 특정 폴더 내의 모든 파일명 앞이나 뒷부분에 원하는 내용을 추가하고자 합니다. 이 경우 다음과 같은 명령어를 입력해주면 폴더 내의 모든 파일명의 prefix(접미사)부분에 추가한 명칭이 추가되는 것을 확인해봅니다.
dir -exclude "1st_*" | Rename-Item -NewName {"1st_" + $_.name}
여기서 위의 명령어들을 하나씩 살펴보도록 하겠습니다.
dir: 폴더 내의 모든 파일을 조회합니다. 만약 폴더 내 하위 폴더의 내용들을 모두 보고 싶다면 다음과 같이 \b\s를 추가해줍니다.
dir \b\s -exclude "1st_*" | Rename-Item -NewName {"1st_" + $_.name}
-exclude "1st_*": 폴더 내 파일명중 "1st_"로 시작되는 파일명은 조회에서 제외합니다. 이때 *은 "1st_" 뒤는 어떤 내용이든 상관없다는 의미로 이해하시면 됩니다.
위 명령어를 미리 넣어주는 이유는 파일명이 변경되고나서도 파일을 또다시 조회하는 경우가 발생하는데 이 경우가 생기면 파일명이 한도끝도 없이 변경되는 참사가 발생하는 경우가 있습니다.
|: 둘 이상의 명령어를 연결해줍니다. 위의 예제에서의 경우 dir을 실행한 다움 Rename-Item 명령어로 이어주어 명령어가 실행될 수 있도록 하여줍니다.
Rename-Item: 지정된 파일명을 변경합니다. 위의 경우 dir로 나타난 결과를 변경합니다.
-NewName {"1st_" + $_.name}: 지정된 파일에 새 이름을 부여합니다. 여기서 "$_name"은 지정된 파일의 이름을 뜻합니다.
위 명령어를 실행하면 아래와 같은 결과를 얻을 수 있습니다.
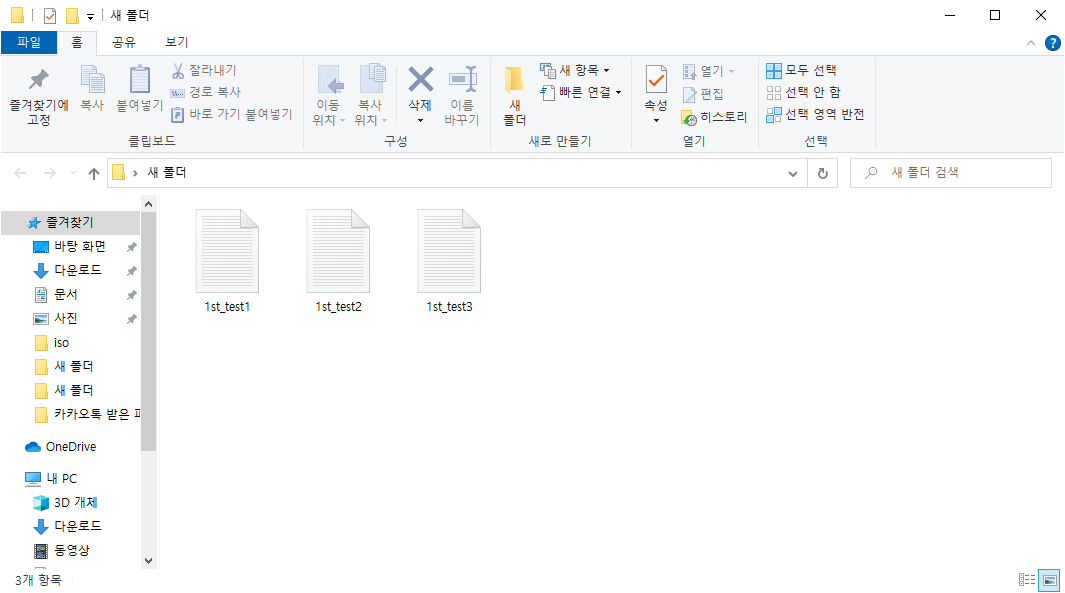
이번에는 파일명의 반복되는 일부분을 변경하는 명령어를 실행해 보겠습니다.
dir | Rename-Item -NewName {$_.name -replace "1st_", "2"}
위 명령어를 보았을 때 -replace가 이름의 일부분을 바꾸는 것임을 유추할 수 있습니다. 명령어를 입력한 후 결과를 확인해 보도록 합니다.
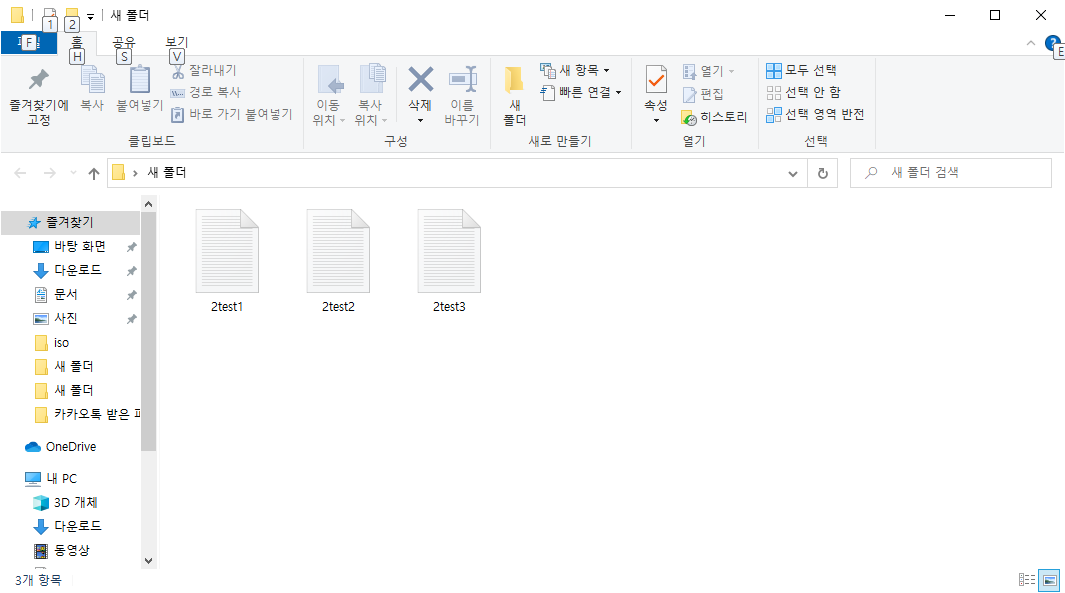
위 예제를 응용하여 이번에는 이름에서 특정 반복되는 부분을 삭제해볼까요?
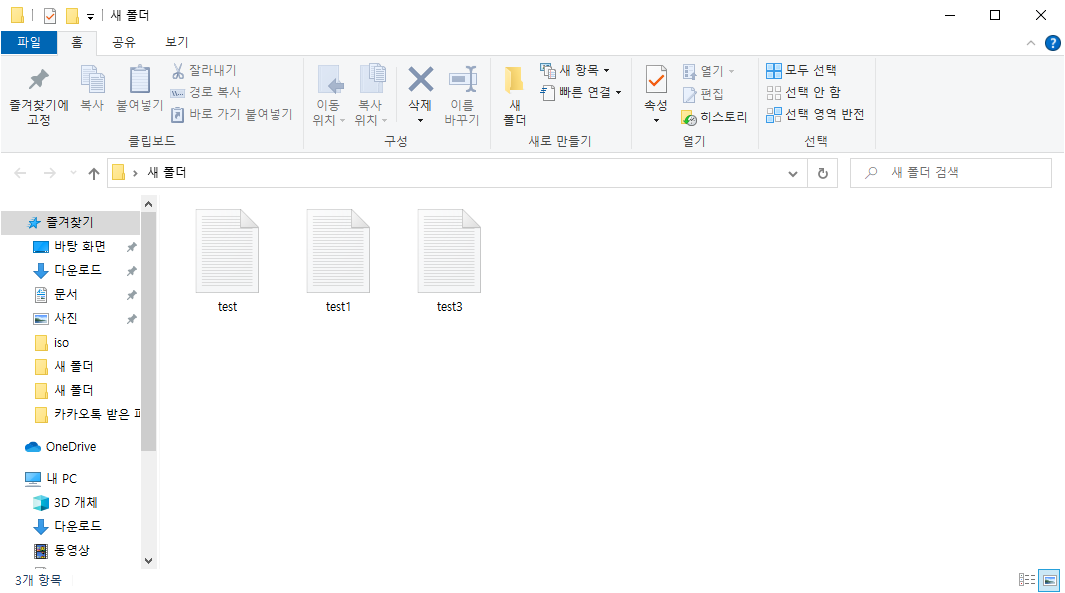
dir | Rename-Item -NewName {$_.name -replace "2", ""}
해당 명령어를 적용해보면 모든 파일의 이름이 말끔하게 바뀌었음을 확인할 수 있습니다.
'공대생의 팁' 카테고리의 다른 글
| Fedora 패키지 저장소 dnf 속도 빠른 서버 자동 설정 방법 (0) | 2021.08.11 |
|---|---|
| VMware에 안드로이드 설치 도중 부팅이 멈출 때 해결방법 (4) | 2021.08.01 |
| VMware에서 Fedora에 VMware Tools 설치 후에도 해상도 변경이 안될때 (0) | 2021.05.16 |
| Windows Powershell 명령어를 바로가기로 구현하기 (1) | 2021.04.30 |
| 부팅시 grub가 화면에 나오지는 않으나 정상적으로 동작할 때 해결방법 (0) | 2021.03.23 |
설정
트랙백
댓글
글
VMware에서 Fedora에 VMware Tools 설치 후에도 해상도 변경이 안될때
다수의 분들이 Linux 운영체제로 우분투를 선택하기에 우분투를 사용하다 발생하는 이슈 및 문제점들을 찾는데 어려움 없이 해결할 수 있지요. 그러함에도 종종 Fedora를 사용하는 경우가 있었는데 Fedora를 사용하는 도중에 발생된 이슈를 처리함에 있어 우분투에 비해 찾기 아려운 점은 항상 아쉬움이 남습니다. 그럼에도 Fedora를 쓰는 이유는 새로운 관점에서 소프트웨어를 사용할 때 어떤 문제가 있을까 하는 점에서 알아보기 위함이 있었습니다.
이번에는 그러한 과정에서 VMware Tools를 설치하였음으에도 Fedora의 해상도가 변하지 않는 현상이 있어 이를 조사하는 과정에서 해결 과정을 기록하고자 합니다.
먼저 기본적으로 VMware Tools를 설치하였을 때 해상도를 자유롭게 바꿀 수 있기에 많이 사용되지요. VMware에 설치된 리눅스에 VMware를 설치하는 방법은 아래의 방법에 따라서 설치해주시면 되겠습니다.
https://recipes4dev.tistory.com/116
VMware Tools 설치 및 업그레이드 방법. (How to install and upgrade the VMware Tools.)
1. VMware Tools 이전 글 [VMware에 우분투 리눅스(Ubuntu Linux) 설치하기]에서 VMware에 우분투 리눅스(Ubuntu Linux)를 설치하는 방법에 대해 설명하였습니다. VMware Workstation Player(버전 12)에 가상 머신..
recipes4dev.tistory.com
희안하게도 Fedora에서는 VMware Tools를 설치하고 나서도 해상도 변경이 되지 않는 점이 있었습니다.
해당 문제의 원인은 Wayland에 관한 이슈가 있는 것으로 보입니다. 해당 문제는 다른 Linux 운영체제에서도 발생할 수 있는 이슈로 추정됩니다.
The issue is that libresolutionKMS.so is not loaded into the Wayland session on Fedora 33
이를 해결하기 위해 vmware tools에서 설정을 일부 변경해주도록 해야 합니다.
1. 먼저 다음과 같은 명령어를 사용해 tools.conf 파일을 생성합니다.
$cp /etc/vmware-tools/tools.conf.example /etc/vmware-tools/tools.conf
2. vi 혹은 gedit와 같은 editor을 실행하여줍니다.
#sudo gedit /etc/vmware-tools/tools.conf
3. [resolutionKMS] 부분을 찾으신 다음 'enable=true' 앞에 있는 주석 '#'을 지운 다음 저장합니다.
[resolutionKMS]
# Default is true if tools finds an xf86-video-vmware driver with
# version >= 13.2.0. If you don't have X installed, set this to true manually.
# This only affects tools for Linux.
enable=true
4. system control을 재시작하여줍니다.
systemctl restart vmtoolsd.service
여기까지 진행하셨다면 VMware에서 Fedora의 해상도를 자유롭게 변환하실 수 있습니다.
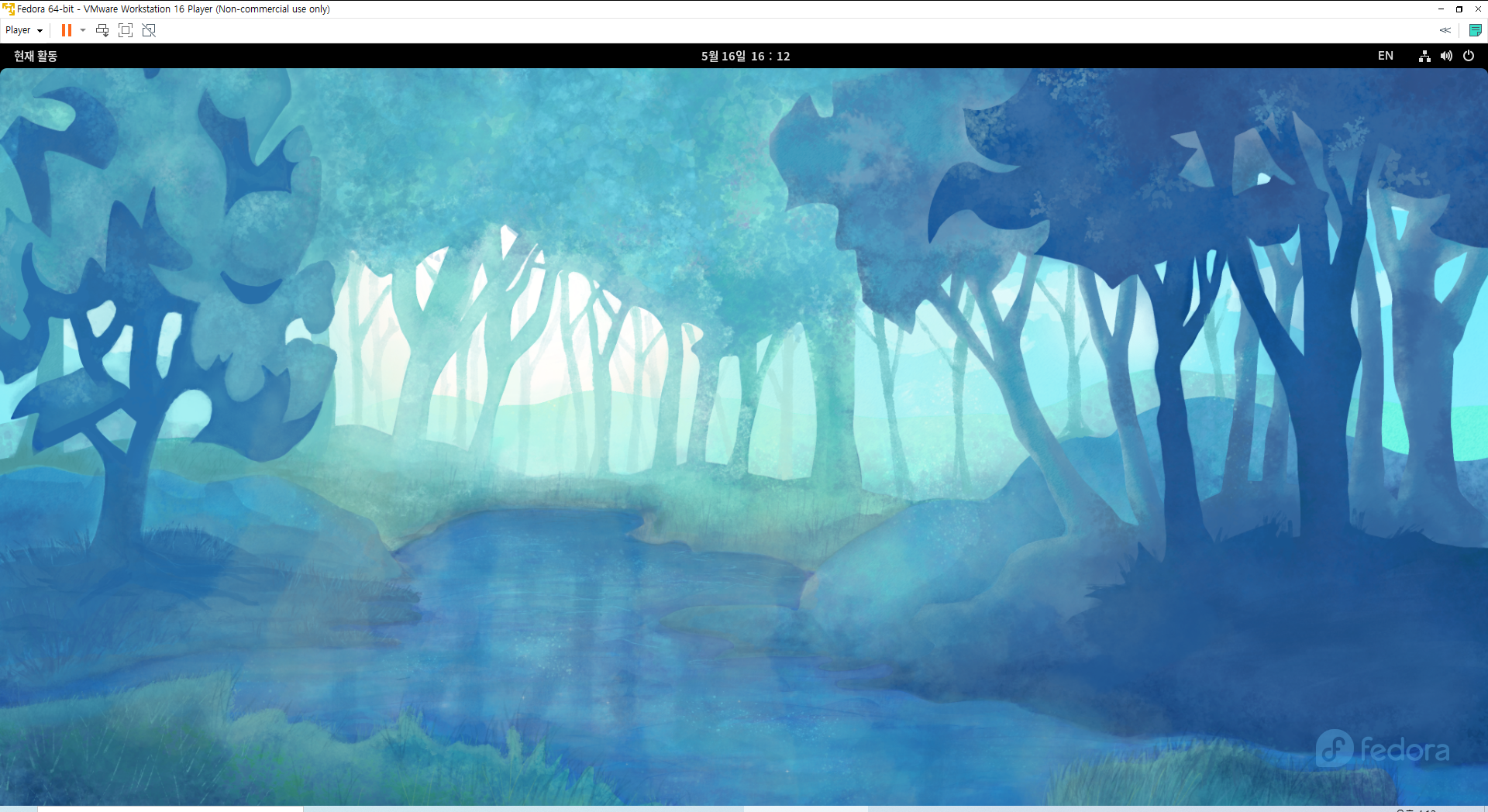
참고자료: https://www.reddit.com/r/Fedora/comments/iygcup/fedora_33_openvmtools/
Fedora 33 open-vm-tools
Can't get f33 to run in full screen under vmware. I checked the open-vm-tools version, it's the same with the one installed in Ubuntu 20.10...
www.reddit.com
'공대생의 팁' 카테고리의 다른 글
| VMware에 안드로이드 설치 도중 부팅이 멈출 때 해결방법 (4) | 2021.08.01 |
|---|---|
| PowerShell을 사용하여 폴더 내의 파일명을 한 번에 바꾸기 (0) | 2021.06.11 |
| Windows Powershell 명령어를 바로가기로 구현하기 (1) | 2021.04.30 |
| 부팅시 grub가 화면에 나오지는 않으나 정상적으로 동작할 때 해결방법 (0) | 2021.03.23 |
| python에서 pip install 과정에서 SSL 오류 해결방법 (0) | 2021.03.16 |
설정
트랙백
댓글
글
Windows Powershell 명령어를 바로가기로 구현하기
인공지능을 Windows에서 다루기 위해 Anaconda를 설치하여 Windows에서도 Python을 사용할 수 있는 기회가 많아지고 있습니다. 그러다보니 자연스레 Ubuntu에서처럼 미리 작성된 스크립트를 바로 실행시켜보고자 하는 방법을 알아보게 되었습니다.
마침 Windows Powershell에서 이와 같은 기능을 사용할 수 있을 것으로 보여 방법을 찾아보았습니다. 혹시나 해당 방법을 필요로 하시는 분들을 위해 방법을 공유해드리겠습니다.
1. Powershell 바로가기 만들기
바탕화면에 Powershell 바로가기를 만드는 방법은 두 가지 경우가 있습니다.
방법1: 바로가기 복사하기
시작버튼 오른쪽에 위치한 돋보기 버튼을 클릭하여 'powershell'이라고 검색하면 아래와 같은 화면을 보실 수 있습니다.
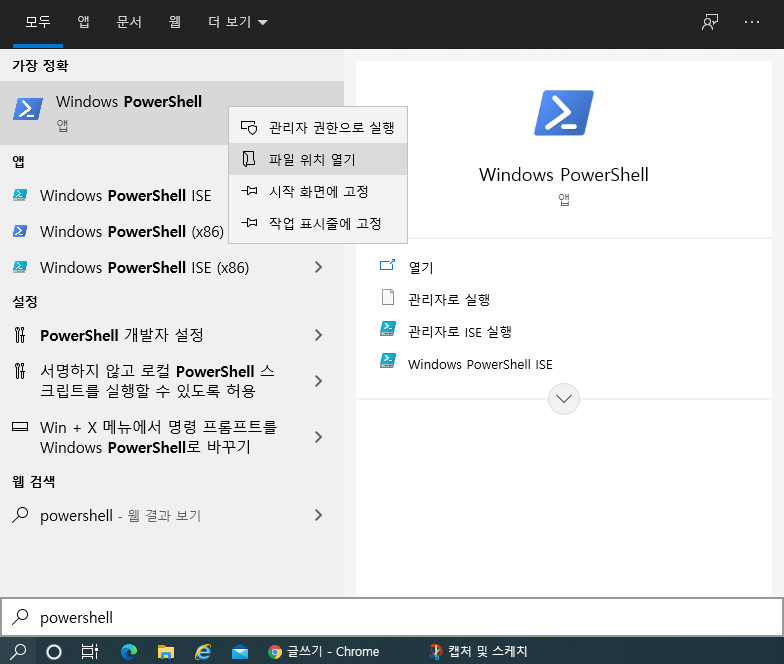
'Windows Powershell' 메뉴에 마우스 오른쪽 버튼을 클릭한 다음 '파일 위치 열기'를 클릭합니다.
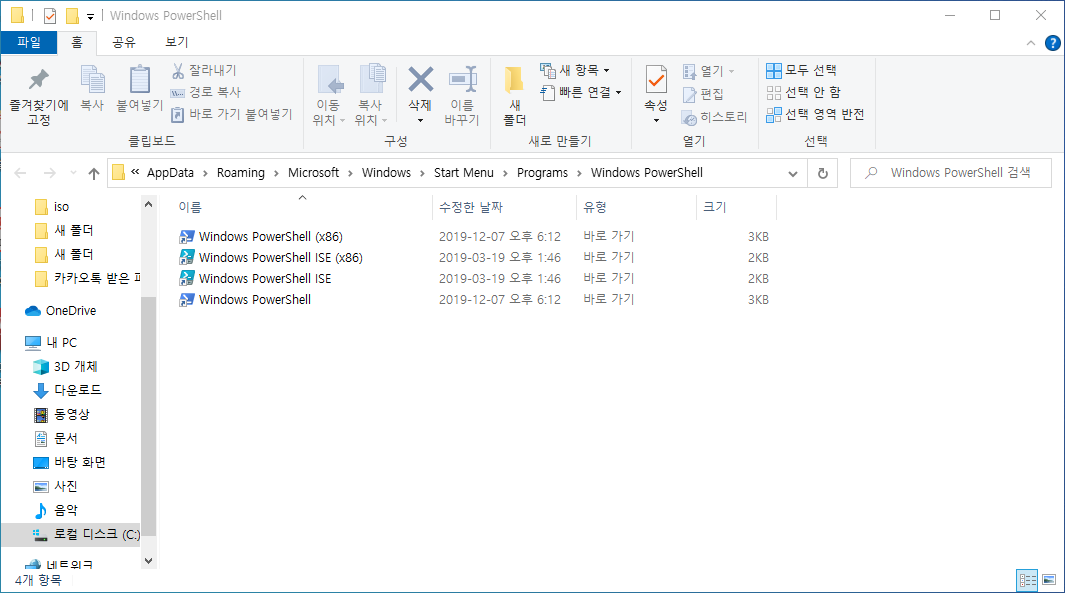
위와 같은 PowerShell 바로가기 아이콘들을 볼 수 있습니다. 이 중 제일 아래의 것을 복사하여 원하는 위치에 붙여넣기를 해주면 됩니다.
방법2: 직접 바로가기 생성
바로가기를 두고싶은 폴더 혹은 바탕화면에서 오른쪽 버튼을 클릭하신 후 '새로 만들기(W)' → '바로 가기(S)'를 선택합니다.
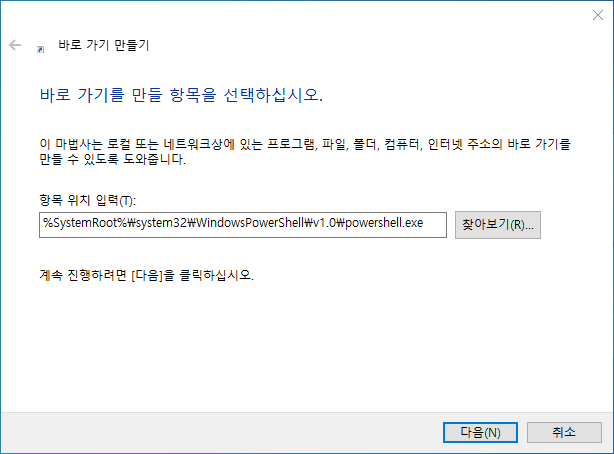
바로 가기 만들기의 항목 위치 입력(T)에 다음과 같은 주소를 입력한 후 다음(N) 버튼을 눌러주세요.
%SystemRoot%\system32\WindowsPowerShell\v1.0\powershell.exe
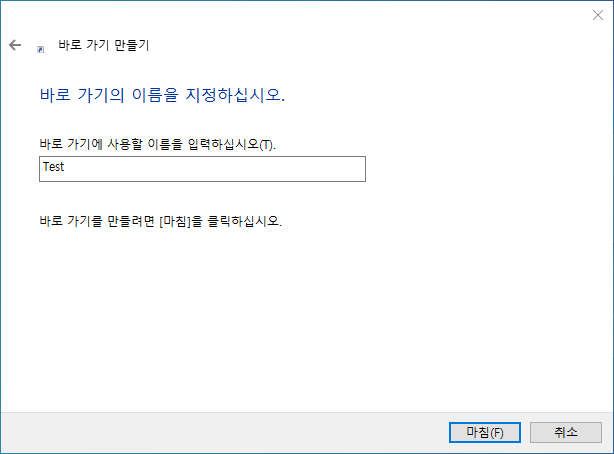
바로가기의 이름을 지정합니다. 이 이름은 PowerShell 창을 열었을 때 창의 제목이 됩니다.
위와 같은 과정을 통해 두 가지의 PowerShell 바로가기를 생성하였습니다. 만약 PowerShell을 실행하자마자 원하는 폴더 경로에 PowerShell을 시작하고 싶으시다면 바로가기의 속성을 변경해줍니다.
2. PowerShell 실행 위치 설정
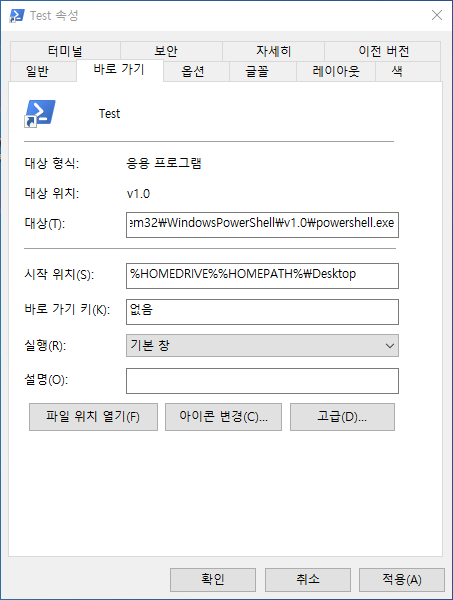
속성에서 '바로 가기' 탭을 선택해 시작 위치(S)에 PowerShell이 시작되었을 때 위치를 설정해줍니다. 위와 같이 설정하실 경우 PowerShell이 실행되자마자 바탕화면에서 PowerShell이 시작됩니다.
3. PowerShell 스크립트 작성하기
지금부터 PowerShell 명령어를 바로 실행할 수 있는 스크립트를 만들어보도록 하겠습니다. PowerShell이 실행되는 스크립드를 메모장으로 다음과 같이 작성하였습니다.
powershell -ExecutionPolicy ByPase -NoExit -Command "& winver;"
여기서 명령어 내용에 대해 간단하게 분석해드리자면
powershell: PowerSehll을 실행합니다.
-ExecutionPolicy: Script 실행 정책을 정의합니다. ByPass를 설정함으로서 직접 입력하지 않아도 해당 명령어를 사용할 수 있도록 해줍니다.
-NoExit: PowerShell 수행이 종료되거나 오류가 발생하더라도 창이 저절로 꺼지지 않게 해줍니다.
-Command: PowerShell에서 수행하고자 하는 명령어를 입력해줍니다. Enter로 나누어지는 명령의 경우 세미콜론(;)으로 구분해줍니다. 양식은 "& 명령어; 명령어;" 식으로 입력해줍니다.
4. 스크립트를 바로가기로 연결하기
다음으로 PowerShell의 바로가기를 수정하여 스크립트가 바로 실행될 수 있도록 설정해줍니다. 해당 바로가기의 속성에서 다음과 같이 수정해줍니다.
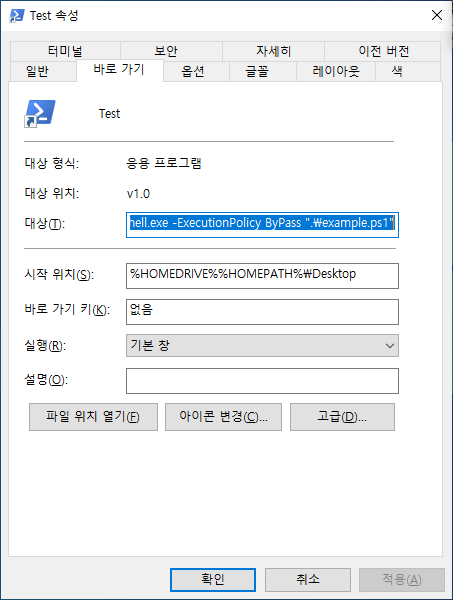
대상(T) 부분에 다음과 같은 내용을 추가하여 example.ps1 스크립트가 실행될 수 있도록 설정합니다.
%SystemRoot%\system32\WindowsPowerShell\v1.0\powershell.exe -ExecutionPolicy ByPass ".\example.ps1"
위와 같이 설정된 PowerShell 바로가기를 실행하면 설정된 명령어가 바로 실행됨을 확인하실 수 있습니다.
'공대생의 팁' 카테고리의 다른 글
| PowerShell을 사용하여 폴더 내의 파일명을 한 번에 바꾸기 (0) | 2021.06.11 |
|---|---|
| VMware에서 Fedora에 VMware Tools 설치 후에도 해상도 변경이 안될때 (0) | 2021.05.16 |
| 부팅시 grub가 화면에 나오지는 않으나 정상적으로 동작할 때 해결방법 (0) | 2021.03.23 |
| python에서 pip install 과정에서 SSL 오류 해결방법 (0) | 2021.03.16 |
| USB없이 GRUB2를 통해 ISO파일 부팅하기(DVD 없이 우분투 설치) (0) | 2021.03.11 |
설정
트랙백
댓글
글
부팅시 grub가 화면에 나오지는 않으나 정상적으로 동작할 때 해결방법
종종 다양한 환경의 컴퓨터에 새로운 환경을 사용하기 위해 운영체제를 새로 설치하여 원하는 환경을 구축하곤 합니다. 컴퓨터마다 설치된 사양과 환경등이 제각각이지만 운영체제를 새로 설치하고나서 부터는 어느 정도 해당 환경에 맞추어 나가다 보면 어느덧 컴퓨터가 손에 길들여지는 것이 느껴지고는 합니다.
그런데 이번에 설치를 시도하게 된 컴퓨터는 유독 희안한 증상이 있었습니다. 우분투도 처음부터 새롭게 설치했음에도 멀티부트 환경 등에서 사용되는 grub 화면이 나오지 않는 것입니다.
대개 거의 대부분의 경우 이는 grub 설정에서 화면을 띄우기도 전에 바로 우분투가 부팅되는 경우이기 때문에 다음과 같이 설정하면 grub 화면이 나타납니다.
# sudo vi /etc/default/grub
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
# If you change this file, run 'update-grub' afterwards to update
# /boot/grub/grub.cfg.
# For full documentation of the options in this file, see:
# info -f grub -n 'Simple configuration'
GRUB_DEFAULT=0
GRUB_TIMEOUT_STYLE=menu
GRUB_TIMEOUT=10
GRUB_DISTRIBUTOR=`lsb_release -i -s 2> /dev/null || echo Debian`
GRUB_CMDLINE_LINUX_DEFAULT="quiet splash"
GRUB_CMDLINE_LINUX=""
# Uncomment to enable BadRAM filtering, modify to suit your needs
# This works with Linux (no patch required) and with any kernel that obtains
# the memory map information from GRUB (GNU Mach, kernel of FreeBSD ...)
#GRUB_BADRAM="0x01234567,0xfefefefe,0x89abcdef,0xefefefef"
# Uncomment to disable graphical terminal (grub-pc only)
#GRUB_TERMINAL=console
|
ddcs |
위의 코드에서 해당 부분에 시간을 부여해주면 grub 메뉴들을 볼 수 있습니다.
GRUB_TIMEOUT=10
그런데 이번에 제가 다루게 된 컴퓨터는 희안하게도 grub 화면에 나타나지 않는 것입니다. 혹시나 해서 grub가 실행되고 있을법한 타이밍에 방향키를 누른 다음 엔터키를 눌러보았는데 희안하게도 해당 메뉴가 실행되는 것을 눈으로 직접 확인하였습니다. 즉, 모종의 이유로 grub가 실행이 되고 있음에도 화면에서는 나타나지 않는 현상으로 보였습니다. 왠지 해당 컴퓨터의 그래픽 출력 관련 문제인 것으로 보아 다음과 같이 다시 시도해 보았습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
# If you change this file, run 'update-grub' afterwards to update
# /boot/grub/grub.cfg.
# For full documentation of the options in this file, see:
# info -f grub -n 'Simple configuration'
GRUB_DEFAULT=0
GRUB_TIMEOUT_STYLE=menu
GRUB_TIMEOUT=10
GRUB_DISTRIBUTOR=`lsb_release -i -s 2> /dev/null || echo Debian`
GRUB_CMDLINE_LINUX_DEFAULT="quiet splash"
GRUB_CMDLINE_LINUX=""
# Uncomment to enable BadRAM filtering, modify to suit your needs
# This works with Linux (no patch required) and with any kernel that obtains
# the memory map information from GRUB (GNU Mach, kernel of FreeBSD ...)
#GRUB_BADRAM="0x01234567,0xfefefefe,0x89abcdef,0xefefefef"
# Uncomment to disable graphical terminal (grub-pc only)
GRUB_TERMINAL=console
|
cs |
다음과 같이 해당 부분의 주석을 지워줍니다.
GRUB_TERMINAL=console
해당 커맨드를 활성화 시키면 grub의 터미널 모드를 그래픽 터미널에서 콘솔 터미널로 바꾸어줍니다. 아마도 그래픽 출력 문제로 인해 화면이 나오지 않는 것으로 추정되어 해당 방법을 시도해 보았는데요 이제 변경된 내용을 grub에 적용해줍니다.
# sudo update-grub
# sudo reboot
여기까지 진행한 다음 리셋을 했더니 드디어 grub메뉴가 모니터에서 나타났습니다.
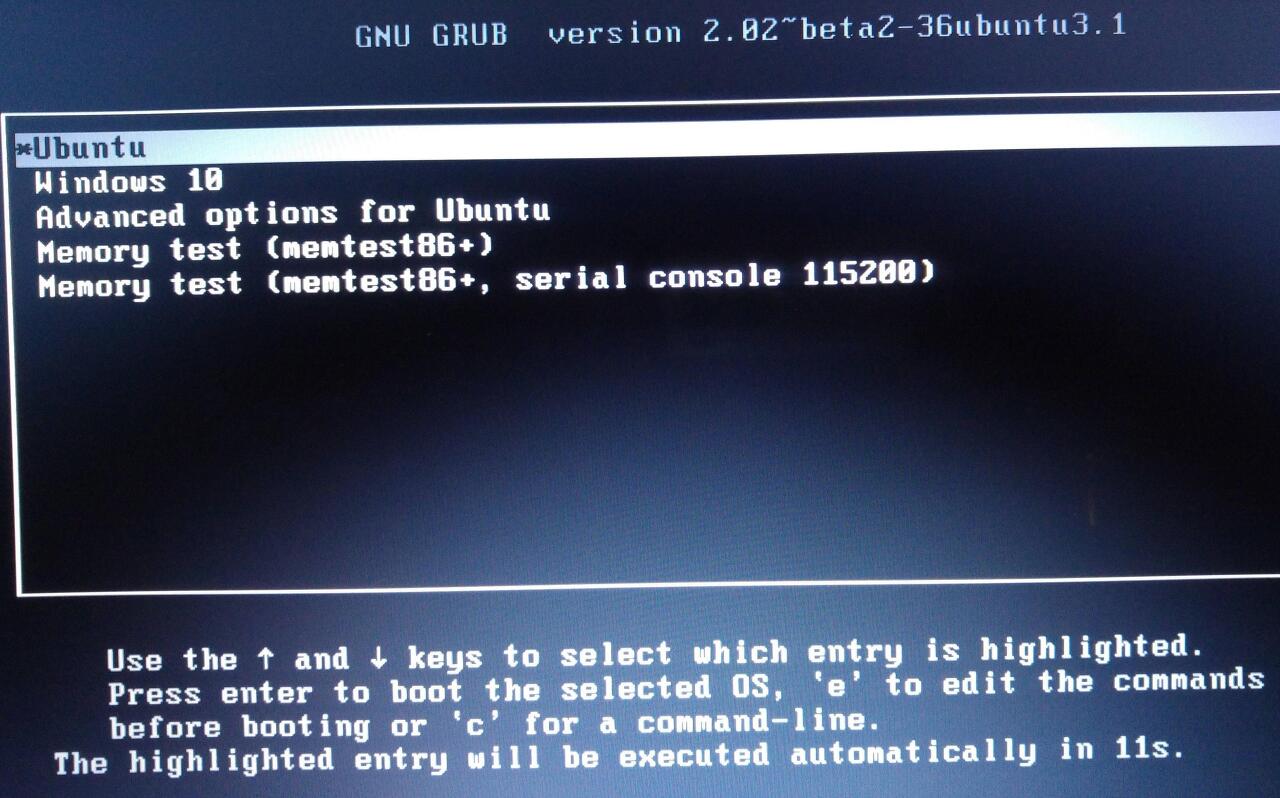
일반적으로 많이 보던 grub의 모습과 달리 완전 새까만 배경의 모습으로 메뉴를 표시합니다. 추정컨데 그래픽 모드가 아닌 콘솔 모드로 출력되어 그래픽카드가 아닌 텍스트 콘솔 출력 방식으로 띄우는 듯 합니다. 그래픽 카드의 문제를 해결해보고 싶었지만 일단 화면이 안나온 것을 해결하였으니 여기서 만족하기로 하였습니다.
해당 원인에 대해 좀 더 자세히 확인하고 싶으신 분들께서는 아래의 포스팅을 참조해 주시기 바랍니다.
Get grub menu back after installing Ubuntu 20.04 alongside Windows
TL;DR
medium.com
'공대생의 팁' 카테고리의 다른 글
| VMware에서 Fedora에 VMware Tools 설치 후에도 해상도 변경이 안될때 (0) | 2021.05.16 |
|---|---|
| Windows Powershell 명령어를 바로가기로 구현하기 (1) | 2021.04.30 |
| python에서 pip install 과정에서 SSL 오류 해결방법 (0) | 2021.03.16 |
| USB없이 GRUB2를 통해 ISO파일 부팅하기(DVD 없이 우분투 설치) (0) | 2021.03.11 |
| Gower's distance(가워 거리) (2) | 2021.02.01 |
설정
트랙백
댓글
글
python에서 pip install 과정에서 SSL 오류 해결방법
python의 라이브러리를 사용함에 있어 pip를 통해 관련 라이브러리 패키지를 다운로드 받아 설치할 수 있습니다. 비록 pip가 root 권한 관련 문제가 있지만 그나마 사용할만한 것입니다. 물론 이러한 문제는 아나콘다의 설치환경 설정으로 어느정도 해결된 감이 있습니다.
pip를 통해 직접 다운로드를 하는 과정에서 내부망의 정책에 의해 제한 등이 있을 경우 아래와 같이 SSL 문제가 발생되는 것을 볼 수 있었습니다. 아래의 예는 Python에서 사용되는 라이브러리인 SciPy를 설치하는 과정에서 발견하게된 오류입니다.
Retrying (Retry(total=0, connect=None, read=None, redirect=None, status=None)) after connection broken by 'SSLError(SSLError(1, '[SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed (_ssl.c:852)'),)': /simple/scipy/
Could not find a version that satisfies the requirement scipy (from versions: )
No matching distribution found for scipy
해당 문제롤 해결하기 위해 pip에서 제공하는 --trusted-host 옵션을 사용합니다. 명령어는 아래와 같습니다.
#Python2
$ python2 -m pip --trusted-host pypi.python.org --trusted-host files.pythonhosted.org --trusted-host pypi.org install 패키지명
# Python3
$ python3 -m pip --trusted-host pypi.python.org --trusted-host files.pythonhosted.org --trusted-host pypi.org install 패키지명
만약 위의 명령어가 너무 길어 차후 설치할 때 일일이 입력하지 않고 간단하게 실행을 원하시는 분은 다음과 같이 .bashrc에 기록해줍니다.
$ vi ~/.bashrc
#Python2
alias pip2='python2 -m pip --trusted-host pypi.python.org --trusted-host files.pythonhosted.org --trusted-host pypi.org'
#Python3
alias pip3='python3 -m pip --trusted-host pypi.python.org --trusted-host files.pythonhosted.org --trusted-host pypi.org'
위와같이 설정하신 후 차후에는 다음과 같이 명령어를 입력하시면 간편하게 Python 라이브러리를 pip를 통해 설치하실 수 있습니다.
#Python2
$ pip2 install 패키지명
#Python3
$ pip3 install 패키지명
※ 2022년 5월 12일 추가
Windows 환경에서 pip의 SSL error 이슈를 해결하기 위해 위에서 설명한바와 같이 --trusted-host로 웹사이트를 추가하여 pip에 적용합니다. 이를 Powershell로 간단하게 적용하는 방법을 아래의 글에서 소개해드리겠습니다.
Windows Powershell로 긴 명령어를 짧게 만드는 function 함수 사용
Windows 환경에서 Python을 사용할 때 pip로 라이브러리를 설치할 때 cmd 혹은 Powershell을 사용합니다. 일반적인 상황에서는 단지 > pip install 라이브러리명 위와 같이 입력만 해줘도 바로 라이브러
elecs.tistory.com
'공대생의 팁' 카테고리의 다른 글
| Windows Powershell 명령어를 바로가기로 구현하기 (1) | 2021.04.30 |
|---|---|
| 부팅시 grub가 화면에 나오지는 않으나 정상적으로 동작할 때 해결방법 (0) | 2021.03.23 |
| USB없이 GRUB2를 통해 ISO파일 부팅하기(DVD 없이 우분투 설치) (0) | 2021.03.11 |
| Gower's distance(가워 거리) (2) | 2021.02.01 |
| 2021년 이후 어도비 플래시 플레이어를 사용하는 방법 (4) | 2021.01.16 |
설정
트랙백
댓글
글
USB없이 GRUB2를 통해 ISO파일 부팅하기(DVD 없이 우분투 설치)
불과 10년전만 해도 CD와 DVD가 쓰이곤 했었는데 어느새부터인가 데스크톱에서 조차 DVD-ROM이 탑재되지 않는 모델들이 등장하고 있습니다. 2021년 기준 32GB짜리 USB메모리를 3천원에 구할 수 있는데다 어느 컴퓨터에나 있는 USB에 꽂아 데이터를 전송하고 변경도 가능한데 굳이 공DVD를 구해 구워서 데이터를 저장할 필요가 없어진 것이지요. 그러다보니 자연스럽게 컴퓨터에 운영체제를 설치하기 위해 USB로 부팅하는 경우가 흔해지고 있습니다. 그만큼 DVD보다 데이터를 다루는 것이 편해서기 때문이겠지요?
이번 포스팅에서는 Linux 환경에서 GRUB2를 수정하여 USB를 사용하지 않고 하드디스크만으로 ISO 파일을 부팅할 수 있도록 설정하는 방법에 대해 알아보도록 하겠습니다.
※Ubuntu 18.04 데스크톱을 기준으로 Ubuntu 20.04 ISO 파일을 설치하는 과정을 다룹니다.
1. 부팅하고자 하는 ISO 파일을 구합니다.
아래의 사이트를 통해 Ubuntu 설치 ISO 파일을 다운로드한 다음 원하는 폴더에 위치하도록 합니다.
http://mirror.kakao.com/ubuntu-releases/
Ubuntu Releases
These older Ubuntu releases are now in Extended Maintenance (ESM): We are happy to provide hosting for the following projects via the cdimage server. While th
mirror.kakao.com
2. ISO파일이 위치한 폴더의 파티션을 확인한다.
다음 명령어를 통해 폴더의 파티션이 어디에 속해있는지 확인할 수 있습니다.
$ df -h
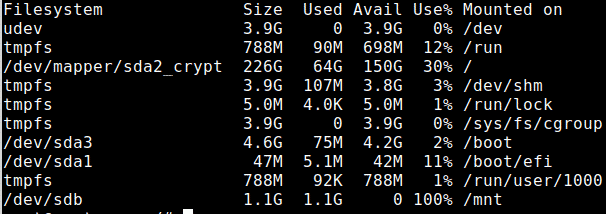
위의 결과에서 Filesystem에서 /dev/sd~~ 라고 써있는 부분이 설치시 필요한 파티션들입니다. 혹시 자신의 파티션이 단 하나일 경우 해당 파티션에 우분투가 설치되어 있어 ISO로 부팅했을 때 해당 파티션을 잡게 되어 새로 설치하는 것이 어렵습니다. 이를 위해서는 단일 파티션을 쪼개 ISO 파일을 위치시킬 파티션을 따로 만들어주어야 합니다. 해당 방법에 대해서는 아래의 링크를 참조해주세요.
리눅스 파티션 설정 ( 파티션 만들기 / 파티션 나누기 )
안녕하세요 롯사입니다. 리눅스를 설치할 때 자동으로 파티션을 구성하여 설치하셨다면 이번엔 리눅스 터미널 환경에서 fdisk라는 명령어를 이용해서 수동으로 파티션을 나누어 보겠습니다. 여
wlsvud84.tistory.com
ISO 파일을 위치시킬 파티션에 ISO파일을 옮긴 후 다음으로 진행합니다.
3.GRUB2에 ISO파일을 등록
다음 명령어를 입력하여 GRUB2에 부팅할 ISO파일을 등록해줍니다.
# sudo vi /etc/grub.d/40_custom
해당 파일에 다음과 같은 내용을 작성해줍니다.
|
1
2
3
4
5
6
7
|
menuentry "Ubuntu 20.04.2 ISO" {
set isofile="/<파일경로>/ubuntu-20.04.2.0-desktop-amd64.iso"
#/dev/sda5에 설치시
loopback loop (hd0,5)$isofile
linux (loop)/casper/vmlinuz.efi boot=casper iso-scan/filename=$isofile noprompt noeject
initrd (loop)/casper/initrd.lz
}
|
cs |
만약 자신의 운영체제가 GRUB 2.04 버전을 사용하고 있을 경우 다음과 같은 내용을 작성해줍니다.
|
1
2
3
4
5
6
7
8
|
menuentry "Ubuntu 20.04.2 ISO" {
set isofile="/<파일경로>/ubuntu-20.04.2.0-desktop-amd64.iso"
rmmod tpm
#/dev/sdc1에 설치시
loopback loop (hd2,1)$isofile
linux (loop)/casper/vmlinuz.efi boot=casper iso-scan/filename=$isofile noprompt noeject
initrd (loop)/casper/initrd.lz
}
|
cs |
위의 코드를 한 줄 씩 살펴보겠습니다.
menuentry "Ubuntu 20.04.2 ISO" {
GRUB 첫 화면에서 메뉴 선택시 제목을 설정합니다. "Ubuntu 20.04.2 ISO"라는 제목으로 메뉴가 표출됩니다.
set isofile="/<파일경로>/ubuntu-20.04.2.0-desktop-amd64.iso"
ISO 파일이 위치한 경로를 선택합니다.

만약 여러분들이 /dev/sdb 파티션에 위치한 ISO 파일을 부팅하기를 원할 때 절대경로는 /mnt/파일명.iso이지만 /dev/sdb의 기본 주소가 /mnt 이므로 파일경로는 /mnt를 생략하고 다음과 같이 작성하면 됩니다.
set isofile="/ubuntu-20.04.2.0-desktop-amd64.iso"
다음으로 파티션 위치를 설정하는 방법에 대하여 설명해보도록 하겠습니다.
loopback loop (hd0,5)$isofile
위의 에서 hd0,5는 파티션 /dev/sda5에 위치한 ISO 파일을 가리키고 있습니다. /dev/sdXY에서 X는 파티션의 알파벳 부분으로 a부터 0으로 카운트되며 Y는 해당 파티션의 번호입니다. ISO 파일이 위치한 파티션을 확인하신 다음 입력하시면 되겠습니다.
정확하게 ISO 파일이 위치한 파티션의 위치를 확인하기 위해 재부팅후 GRUB 화면으로 넘어옵니다.
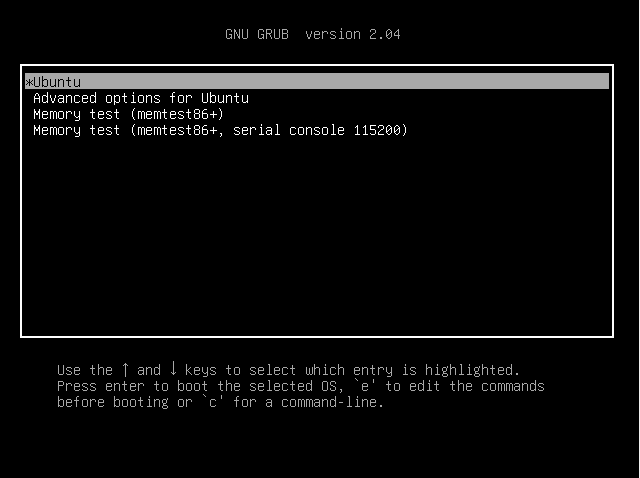
위 화면에서 'c' 버튼을 누르면 GRUB의 커맨드창이 나옵니다. 아래와 같이 명령어를 입력해줍니다.
grub> ls -al
입력후 아래와 같이 컴퓨터에 연결된 파티션 정보가 출력됨을 알 수 있습니다.
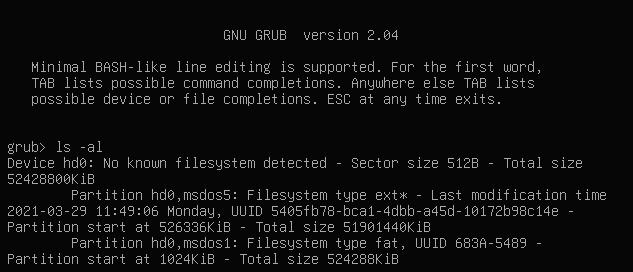
위의 경우 hd0에는 (hd0,msdos5) 파티션과 (hd0,msdos1) 파티션이 존재함을 확인할 수 있습니다. ISO 파일이 어떤 파티션에 있는지 확인하기 위해 다음과 같은 명령어를 입력하면 해당 파티션의 파일 구조를 확인할 수 있습니다.
grub> ls (hd0,msdos5)/

이를 통해 ISO 파일의 파일 경로를 확인후 ISO가 있는 파티션을 입력해줍니다.
4. GRUB2의 메뉴를 확인할 수 있는 대기시간을 확보합니다.
아래의 명령어를 입력합니다.
# sudo vi /etc/default/grub
해당 부분을 다음과 같이 수정하여 GRUB2에서 메뉴를 선택할 수 있는 시간을 확보합니다. 여기서는 10초 할당하였습니다.
GRUB_TIMEOUT=10
5. GRUB2의 설정을 업데이트한 다음 리셋하여 확인
아래의 명령어를 입력하여 GRUB2의 메뉴를 업데이트합니다.
# sudo update-grub
여기까지 진행하셨다면 시스템을 리셋하여 GRUB2 메뉴에 ISO 파일 부팅이 되는 것을 확인합니다.
# sudo reboot
'공대생의 팁' 카테고리의 다른 글
| 부팅시 grub가 화면에 나오지는 않으나 정상적으로 동작할 때 해결방법 (0) | 2021.03.23 |
|---|---|
| python에서 pip install 과정에서 SSL 오류 해결방법 (0) | 2021.03.16 |
| Gower's distance(가워 거리) (2) | 2021.02.01 |
| 2021년 이후 어도비 플래시 플레이어를 사용하는 방법 (4) | 2021.01.16 |
| MobaXterm에서 X server 사용시 전체화면 모드 화면이 안나올때 해결방법 (1) | 2020.10.25 |
설정
트랙백
댓글
글
Gower's distance(가워 거리)
인간의 경험에 있어서 거리의 개념은 직관적으로 예상할 수 있습니다. 측정기준이라는 용어는 종종 측정을 위한 표준으로 사용되는 반면, 일상 생활에서는 일반적으로 두 지점의 물리적인 가까움 또는 아이디어 사이가 어느 정도 되는지의 근접성을 의미합니다. 관측치 사이의 거리 또는 정량적 또는 정성적 변수 사이의 거리를 고려할 수도 있습니다.
데이터를 클러스터링하는 동안 가장 중요한 작업 중 하나는 각 데이터 포인트 사이의 거리를 계산하는 데 사용할 방법을 결정하는 것입니다. 생물학, 사회과학 또는 마케팅 조사와 같이 클러스터 분석이 일반적으로 사용되는 다양한 실제 분야에서는 수치 변수와 카테고리 변수를 모두 갖는 데이터셋이 적용되는 경우가 많습니다. 이러한 유형의 데이터를 혼합 데이터(Mixed data)라고 합니다. 많은 거리 측정방법이 존재하며, 그 중 여기서 소개해드리고자 하는 것은 데이터가 혼합 데이터일 때 사용되는 가워 거리(Gower's distance - 1971)입니다.
가워 거리(Gower's distance)란 무엇인가?
가워 거리(Gower's Distance)는 가워 차이 계수(Gower's dissimilarity coefficient)라고도 하며 사용하여 두 데이터의 차이를 측정할 수 있습니다. 기록에는 논리, 카테고리, 수치 또는 텍스트 데이터의 조합이 포함될 수 있습니다. 거리는 항상 0(동일함)에서 1(가장 큰 차이) 사이의 숫자입니다.
q개의 차원을 가지고 있는 벡터 \(\textbf{x}\)가 있다고 하였을 때 \(\textbf{x}\)가 p개의 카테고리형 변수를 갖고 있다 하였을 때
$$\LARGE{\textbf{x} = (x_1, x_2, ... , x_p, x_{p+1}, ..., x_q)}$$
위 벡터에서 p개의 카테고리형 변수의 q-p개의 수치형 변수가 있다고 하였을 때 해당 식을 아래와 같이 다시 쓸 수 있습니다.
$$\LARGE{\textbf{x} = (z_1, ..., z_p, c_1, ..., c_{q-p})^\top=(\textbf{z}^\top,\textbf{c}^\top)}$$
여기서 벡터 \(\textbf{z}^\top\)와 \(\textbf{c}^\top\)는 벡터 \(\textbf{x}\)의 부분집합입니다. 이 때 두 데이터 포인트 \(\textbf{x}_i=(\textbf{z}_i^\top,\textbf{c}_i^\top)\) 와 \(\textbf{x}_j=(\textbf{z}_j^\top,\textbf{c}_j^\top)\)의 가워 거리 \(D_{x_ix_j}\)를 구하는 식은 다음과 같이 나타낼 수 있습니다.
$$\LARGE{D_{x_{i}x_{j}}=\dfrac{\sum^{p}_{r=1}W_{x_{i}x_{j}z_{r}}D_{x_{i}x_{j}z_{r}}}{\sum^{p}_{r=1}W_{x_{i}x_{j}z_{r}}}+\dfrac{\sum^{q-p}_{r=1}W_{x_{i}x_{j}c_{r}}D_{x_{i}x_{j}c_{r}}}{\sum^{q-p}_{r=1}W_{x_{i}x_{j}c_{r}}}}$$
여기서 \(W_{x_{i}x_{j}z_{r}}\) 와 \(W_{x_{i}x_{j}c_{r}}\) 는 각각 카테고리형 변수 \(z_r\)과 수치형 변수 \(c_r\)에 해당되는 가중치값을 나타냅니다.
\(D_{x_{i}x_{j}z_{r}}\) 카테고리형 변수의 \(z_r\)의 거리를 나타낸 것으로 다음과 같은 식으로 나타냅니다.
$$\LARGE{D_{x_{i}x_{j}z_{r}}=\begin{cases}0,\quad z_{r}^{i}=z_{r}^{j}\\1,\quad otherwize\end{cases}}$$
만약 두 카테고리형 변수가 같은 값일 경우 0, 다른 값일 경우 1이 된다고 이해하면 쉬울 것입니다.
\(D_{x_{i}x_{j}c_{r}}\)은 실수인 수치형 변수로서 우리가 흔히 아는 맨허튼 거리(\(L_1\) norm) 방식으로 값을 구합니다.
$$\LARGE{D_{x_ix_jc_r}=\dfrac{|c_r^i-c_r^j|}{\max(c_r)-\min(c_r)}}$$
위 식을 보았을 때, 각 변수의 차의 절대값에 실수 \(c\)의 범위(최대값 - 최소값)을 나눔으로서 변수의 거리를 알 수 있습니다. 여기서는 맨허튼 거리를 예제로 하였지만 좀 더 좋은 공식이 있다면 그것을 사용해도 무방합니다.
예제
다음과 같은 데이터가 있다고 합시다.
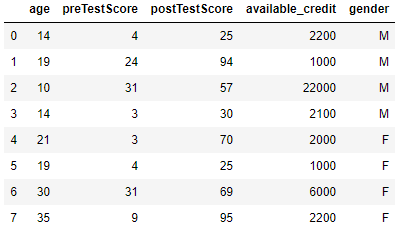
위 데이터를 보았을 때 [age, perTestScore, postTestScore, available_credit] 4개의 변수는 수치형 변수이고 [gender] 1개의 변수는 카테고리형 변수임을 알 수 있습니다. 즉 이를 벡터로 나타내면 다음과 같습니다.
$$\LARGE{\textbf{x} = (c_1, c_2, c_3, c_4, z_1)}$$
이 때 weight를 1이라고 하였을 때 가워 거리는 다음과 같이 나타낼 수 있습니다.
$${D_{x_ix_j}=\dfrac{|c_1^i-c_1^j|}{\max(c_1)-\min(c_1)}+\dfrac{|c_2^i-c_2^j|}{\max(c_2)-\min(c_2)}+\dfrac{|c_3^i-c_3^j|}{\max(c_3)-\min(c_3)}+\dfrac{|c_4^i-c_4^j|}{\max(c_4)-\min(c_4)}+D_{x_{i}x_{j}z_{1}}}$$
주어진 벡터에서 \(x_0\)을 기준으로 각 row별로 가워 거리를 구하면 다음과 같습니다.
$$D_{x_{0}x_{1}}=\dfrac{\left|14-19\right|}{35-10}+\dfrac{\left|4-24\right|}{31-3}+\dfrac{\left|25-94\right|}{95-25}+\dfrac{\left|2200-1000\right|}{22000-1000}+0 \\ = 1.9572$$
$$D_{x_{0}x_{2}}=\dfrac{\left|14-10\right|}{35-10}+\dfrac{\left|4-31\right|}{31-3}+\dfrac{\left|25-57\right|}{95-25}+\dfrac{\left|2200-22000\right|}{22000-1000}+0 \\ = 0.2529$$
$$D_{x_{0}x_{3}}=\dfrac{\left|14-14\right|}{35-10}+\dfrac{\left|4-3\right|}{31-3}+\dfrac{\left|25-30\right|}{95-25}+\dfrac{\left|2200-2100\right|}{22000-1000}+0 \\ = 0.1120$$
$$D_{x_{0}x_{4}}=\dfrac{\left|14-21\right|}{35-10}+\dfrac{\left|4-3\right|}{31-3}+\dfrac{\left|25-70\right|}{95-25}+\dfrac{\left|2200-2000\right|}{22000-1000}+1 \\ = 1.9681$$
$$D_{x_{0}x_{5}}=\dfrac{\left|14-19\right|}{35-10}+\dfrac{\left|4-4\right|}{31-3}+\dfrac{\left|25-25\right|}{95-25}+\dfrac{\left|2200-1000\right|}{22000-1000}+1 \\ = 1.2571$$
$$D_{x_{0}x_{6}}=\dfrac{\left|14-30\right|}{35-10}+\dfrac{\left|4-31\right|}{31-3}+\dfrac{\left|25-69\right|}{95-25}+\dfrac{\left|2200-6000\right|}{22000-1000}+1 \\ = 3.4138$$
$$D_{x_{0}x_{7}}=\dfrac{\left|14-35\right|}{35-10}+\dfrac{\left|4-9\right|}{31-3}+\dfrac{\left|25-95\right|}{95-25}+\dfrac{\left|2200-2200\right|}{22000-1000}+1 \\ = 3.0186$$
위 계산을 보았을 때 \(x_0\)에서 Gower's distance가 가장 가까운 것은 \(x_3\)이고 가장 먼 것은 \(x_6\)임을 알 수 있습니다.
- 참고자료
https://medium.com/analytics-vidhya/gowers-distance-899f9c4bd553
Gower’s Distance
One of the most important task while clustering the data is to decide what metric to be used for calculating distance between each data ….
medium.com
https://jamesmccaffrey.wordpress.com/2020/04/21/example-of-calculating-the-gower-distance/
Example of Calculating the Gower Distance
The Gower distance is a metric that measures the dissimilarity of two items with mixed numeric and non-numeric data. Gower distance is also called Gower dissimilarity. One possible use of Gower dis…
jamesmccaffrey.wordpress.com
Gower Distance
Tuerhong, G., & Kim, S. B. (2014). Gower distance-based multivariate control charts for a ...
blog.naver.com
'공대생의 팁' 카테고리의 다른 글
| python에서 pip install 과정에서 SSL 오류 해결방법 (0) | 2021.03.16 |
|---|---|
| USB없이 GRUB2를 통해 ISO파일 부팅하기(DVD 없이 우분투 설치) (0) | 2021.03.11 |
| 2021년 이후 어도비 플래시 플레이어를 사용하는 방법 (4) | 2021.01.16 |
| MobaXterm에서 X server 사용시 전체화면 모드 화면이 안나올때 해결방법 (1) | 2020.10.25 |
| 여분기여도(Marginal Contribution) (0) | 2020.09.13 |
설정
트랙백
댓글
글
2021년 이후 어도비 플래시 플레이어를 사용하는 방법
1996년 11월 처음으로 등장한 Flash는 매크로미디어가 만들어 2005년 Adobe에 인수된 후 2020년 12월까지 서비스가 제공되었습니다.
처음 등장했던 당시에는 가벼운 용량으로 컴퓨터의 성능이 지금보다 뛰어나지 못했던 그 당시의 시점으로는 매우 훌륭한 그래픽과 영상을 제작할 수 있었던 인터넷 애플리케이션으로 취급되었습니다. 그 덕분에 졸라맨, 마시마로와 같은 플래시 애니메이션이 사람들에게 인기를 끌 수 있었던 시절이 있었지요.
그러나 세월이 흐르면서 플래시가 랜섬웨어에 취약하여 컴퓨터 보안에 매우 치명적인 문제가 발생하였습니다. 또한 크롬을 필두로한 브라우저 경쟁을 거치면서 웹표준이 만들어지면서 플래시는 천덕꾸러기 신세가 되어버리면서 최신 웹브라우저들에서 비활성화 설정되어 점점 사용을 자제하는 분위기가 조성되었고 지원이 종료되는 2020년 12월까지는 보안 패치만 적용되며 연명하고 있었습니다.
그렇게 2021년 1월 12일을 기점으로 모든 웹브라우저에서 플래시가 더이상 작동되지 않도록 설정되어 이제는 영원히 역사속으로 사라졌습니다.
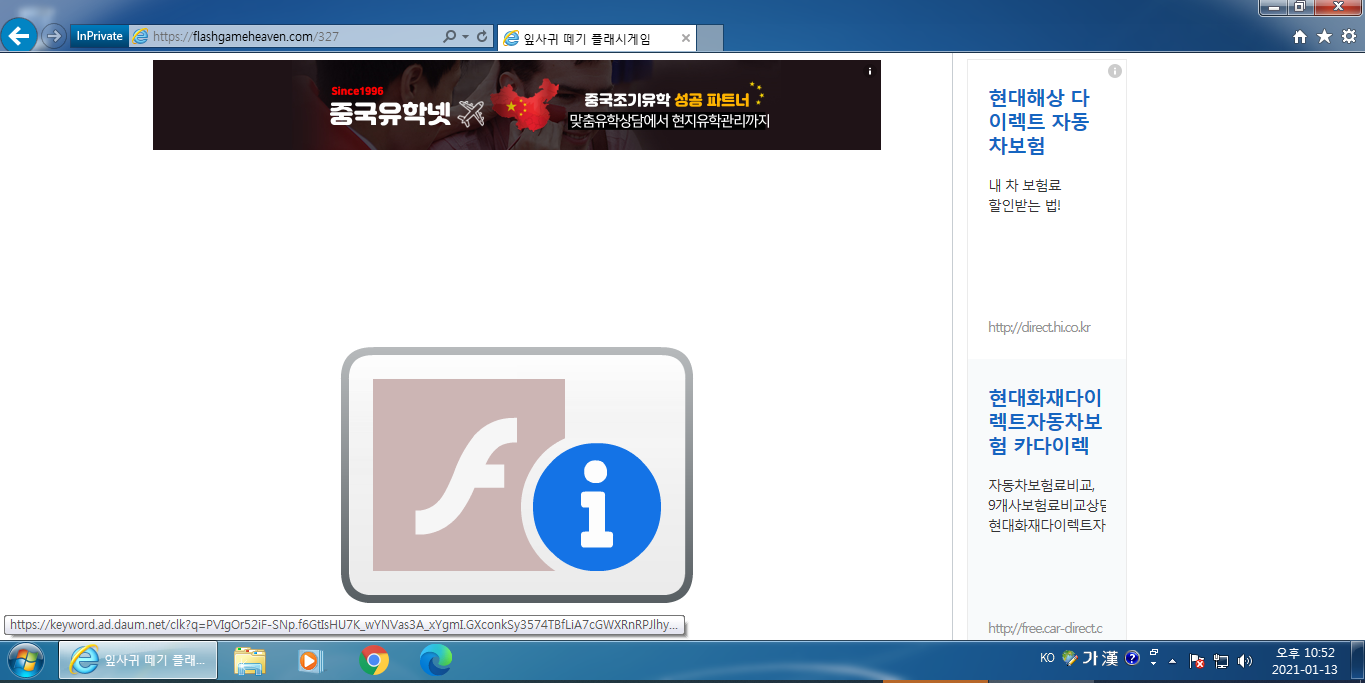
위에서 보시는 바와 같이 플래시가 적용되어 있는 웹페이지는 위와 같은 모습으로 더이상 플래시를 사용할 수 없음을 사람들에게 알리게 되었습니다. 이렇게 플래시는 인터넷 역사의 한 장을 마감하게 되었지요.
그러나 몇몇 사이트들의 경우 플래시를 여전히 사용하고 있고 이를 사용해야만 하는 경우 매우 곤란한 상황이 벌어지게 되었지요. 사전에 플래시가 없는 환경을 구축하였어야 하지만 부득이하게 이러한 플래시 환경에서 작업을 하셔야 하는 분들께 2021년 이후 플래시를 사용할 수 있는 방법에 대해 알려드리고자 합니다.
※현재 Flash Player가 종료되어 보안 관련 문제 위험을 최소화하고자 이 글에서는 가상머신을 통한 사용 방법을 설명드리고 있습니다. 만약 가상머신을 사용하지 않고 자신의 컴퓨터에 직접 Flash Player를 사용하고자 하시는 분은 아래의 글을 참조해주시기 바랍니다.
Windows 11에서 어도비 플래시 플레이어를 사용하는 방법
지난 1월 12일, 어도비의 플래시 플레이어 서비스가 종료되면서 최신 버전의 플래시 플레이어가 설치되었던 컴퓨터에서 더이상 플래시를 사용할 수 없게 되었습니다. 이를 극복하기 위해 가상
elecs.tistory.com
※Windows 10 최신 버전에서는 업데이트 자체에서 Flash player의 설치를 더이상 허용하고 있지 않습니다. 구버전 설치를 시도할 경우 아래와 같이 설치가 더이상 진행되지 않고 있습니다. Windows 10에서의 Internet Explorer 내에는 Flash Player가 내장되어 있어 설치를 별도로 할 수 없는 것입니다.

이를 해결하기 위해 저는 Windows 7을 다시 설치하여 진행하였음을 알립니다. 혹시 Windows 7을 설치하고자 하시는 분은 아래의 사이트를 통해 Windows 7 설치 ISO를 받으신 다음 설치를 진행해주세요.
https://extrememanual.net/7885
윈도우7 포함 모든 버전 순정 ISO 파일 다운로드 방법 - 익스트림 매뉴얼
윈도우7 순정 이미지를 다운로드 받으려고 검색을 해보면 대부분 토렌트 같은 P2P 프로그램이나 웹하드같은 사이트에서 다운로드 받아야 하는데 토렌트로 배포되는 윈도우7 ISO 이미지 같은 경우
extrememanual.net
ISO 설치 파일을 받으신 다음 자신이 원하는 PC에 Windows 7을 설치해 보도록 합니다.
https://extrememanual.net/11423
윈도우7 클린 설치 방법 USB 부팅부터 설치까지 - 익스트림 매뉴얼
컴퓨터를 새로 구매하거나 기존에 사용하던 윈도우가 정상 작동을 하지 않는 경우, 설치한지 오래된 경우 프로그램을 자주 깔고 삭제하면 불필요한 레지스트리가 남게 되는데 이럴때는 문제점
extrememanual.net
만약 자신의 컴퓨터에 Windows 7을 직접 설치하고 싶으신 경우 멀티부팅 혹은 가상머신을 활용하여 설치하여 사용할 수 있습니다. 멀티부팅 설정법과 가상머신 사용법은 아래의 링크를 참조해 주시기 바랍니다.
자신의 컴퓨터에 멀티부팅으로 Windows 7 설치방법
https://stainpopper.tistory.com/97
윈도우 10과 7을 동시에 사용할 수 있도록 듀얼 부팅 만드는방법
한대의 컴퓨터에 윈도우 7과 윈도우 10을 동시에 설치 하여 윈도우 10과 7을 동시에 사용할 수 있도록 윈도우10 윈도우7 듀얼 부팅 만드는방법 입니다. 먼저 컴퓨터에 윈도우10이 설치되어 있어
stainpopper.tistory.com
가상머신을 활용하여 Windows 7을 활용하는 방법
[VMware] Windows 7 64Bit 설치하기
[VMware] Windows 7 64Bit 설치하기 실습 환경 VMware Workstation 15 Player (FREE 버전) Windows 7 64Bit 저희 블로그에서는 Windows 7 ISO 파일을 제공하지 않습니다. VMware Workstation 15 Player를 실행합니..
nan491.tistory.com
https://blog.naver.com/PostView.nhn?blogId=hong0303&logNo=221258116325
버추얼박스 윈도우7 설치 따라해봐요
버추얼박스에 윈도우7을 설치 해보겠습니다. 윈도우는 7, 8 또는 이전XP라도 설치가 가능합니다. 그외에 ...
blog.naver.com
위의 방법으로 Windows 7 설치 환경을 구성하셨다면 절대로 업데이트를 하여서는 안됩니다. 최신버전으로 업데이트하게 될 경우 Adobe Flash Player의 구버전 설치가 막히게 됩니다.
여기까지 진행하셨다면 다음으로 Flash Player 32.0.0.363 이전의 구버전을 설치합니다. 해당 버전은 구글 검색을 통해 쉽게 구하실 수 있습니다.
https://kbench.com/software/?q=node/77021
Adobe Flash Player v32.0.363 정식버전 (인터넷 익스플로러) | 케이벤치
Adobe Flash Player 플러그인은 웹 브라우저에서 웹 사이트에서 제공되는 플래쉬 무비, 게임 등 플래쉬 컨텐츠를 재생 할 수 있도록 해주는 기능을 가지고 있습니다. 이 프로그램은 인터넷 익스플로
kbench.com
https://drive.google.com/file/d/15ret5DZLTLaFzNPOmNY7NbEINcFKdsEa/view?usp=sharing
install_flash_player_ax_32.0.0.363.exe
drive.google.com
여기까지 진행하셨으면 다음으로 Windows 7에 플래시 플레이어 32.0.0.363 설치해 보도록 하겠습니다.


만약 업무 용도가 아닌 플래시 플레이어 사용이 목적이실 경우 러플(Ruffle)을 설치하여 Chrome, Firefox 등에서 사용하실 수 있습니다. 다만 Flash player를 완벽하게 지원된다고 장담 드리기 어렵습니다. 아래의 사이트를 통해 사용 방법을 확인해주시기 바랍니다.
https://flashgameheaven.com/370?category=947922
2020년 플래시 중단 후 플래시게임하는 방법
어도비 플래시 플레이어(Adobe Flash Player) 플러그인의 지원이 2020년 12월 31일에 종료되었습니다. 어도비 플래시 지원 종료 이후에는 각종 플래시로 제작된 것들은 웹 브라우저에서 재생할 수 없게
flashgameheaven.com
'공대생의 팁' 카테고리의 다른 글
| USB없이 GRUB2를 통해 ISO파일 부팅하기(DVD 없이 우분투 설치) (0) | 2021.03.11 |
|---|---|
| Gower's distance(가워 거리) (2) | 2021.02.01 |
| MobaXterm에서 X server 사용시 전체화면 모드 화면이 안나올때 해결방법 (1) | 2020.10.25 |
| 여분기여도(Marginal Contribution) (0) | 2020.09.13 |
| Chernoff bound(체르노프 유계) (0) | 2020.09.12 |
설정
트랙백
댓글
글
MobaXterm에서 X server 사용시 전체화면 모드 화면이 안나올때 해결방법
리눅스 혹은 임베디드 시스템과 통신할 때 주로 Putty를 사용했던 기억이 있습니다. 원격 접속이 설정이 매우 간단해서 SSH 접속을 하기 위해 자주 사용해왔었습니다.
다만 Putty는 CLI 커맨드 기반의 작업을 수행할 때는 쓸만하지만 요즘같이 GUI 그래픽 기반의 화면을 사용하기 위해서는 Xming과 같은 별도의 프로그램을 설치해서 X11 이미지를 사용할 수 있습니다.
그런데 이번에 소개해드릴 MobaXterm의 경우 터미널과 X11 서버를 하나의 프로그램에서 지원해줘서 이전처럼 X11 전용 프로그램을 별도로 설치하지 않고도 곧바로 GUI 기반 프로그램을 실행할 수 있었습니다.
MobaXterm에서 터미널에 명령어를 수행하면 곧바로 GUI 기반 프로그램이 동작하는 것을 보면 상당히 편하다는 것을 알 수 있습니다. 다만, MobaXterm의 초기 설정대로 전체화면으로 돌아가는 프로그램을 수행하게 되었을 때 화면이 갑자기 사라져 버리는 모습을 볼 수 있습니다.

분명 프로그램은 실행되고 있으나 MobaXterm의 초기 설정 상태에서는 X11이 Multiwindow 모드로 동작하고 있을 때 이러한 문제가 나타나는 것으로 보입니다. 이를 해결하기 위해 MobaXterm에 X11 관련 설정을 수정해줘야 합니다.

MobaXterm에서 'Settings' 버튼을 클릭합니다.

'X11' 탭을 클릭한 후 'X11 server display mode' 부분에서 초기 설정이 "Multiwindow mode"로 되어있는 것을 보실 수 있습니다. 여기서 'Windowed mode'를 선택해줍니다.
X11 설정 변경시 X11 서버를 다시 실행하게 됩니다. '예(Y)' 버튼을 클릭하신 후 잠시 기다리시면 다음과 같이 검은 창이 하나 나타나는 것을 확인하실 수 있습니다.

이제 이 화면에서 UI 관련 프로그램들이 모두 동작하는 것을 확인할 수 있습니다.

이제 전체화면으로 동작하는 프로그래밍을 실행하면 아래와 같이 화면이 바로 사라지지 않고 사용할 수 있게 되는 것을 확인하실 수 있습니다.
'공대생의 팁' 카테고리의 다른 글
| Gower's distance(가워 거리) (2) | 2021.02.01 |
|---|---|
| 2021년 이후 어도비 플래시 플레이어를 사용하는 방법 (4) | 2021.01.16 |
| 여분기여도(Marginal Contribution) (0) | 2020.09.13 |
| Chernoff bound(체르노프 유계) (0) | 2020.09.12 |
| wget 사용시 증명서(certificate) 관련 문제가 발생하였을 때 해결방법 (0) | 2020.09.11 |
설정
트랙백
댓글
글
여분기여도(Marginal Contribution)
게임이론의 관점에서 여분기여도(Marginal Contribution)은 다음과 같이 정의합니다.
플레이어를 맴버로 하는 그룹의 가치에 플레이어가 없는 그룹의 가치를 뺀 다음 플레이어가 혼자 일하는 것에 의해 창출되는 가치를 뺀 값
이를 섀플리값(Shapley Value)의 관점에서는 다음과 같이 표현됩니다.
플레이어 A가 플레이어 B와 연합하여 A와 B의 총 보상이 5라고 하였을 때(즉, \(v(A,B)=5\))
만약 B 혼자서 일을 하였을 때 B의 보상이 2라 한다면\(v(B)=2\), A의 이 연합 {A,B}에 대한 여분기여도는 다음과 같이 계산된다.
$$A의 {A,B}에 대한 기여 = v(A,B)-v(B)=5-2=3$$
'공대생의 팁' 카테고리의 다른 글
| 2021년 이후 어도비 플래시 플레이어를 사용하는 방법 (4) | 2021.01.16 |
|---|---|
| MobaXterm에서 X server 사용시 전체화면 모드 화면이 안나올때 해결방법 (1) | 2020.10.25 |
| Chernoff bound(체르노프 유계) (0) | 2020.09.12 |
| wget 사용시 증명서(certificate) 관련 문제가 발생하였을 때 해결방법 (0) | 2020.09.11 |
| WSL(Windows Subsystem for Linux )에서 'Can't open display: :0.0' 오류 발생시 해결방법 (1) | 2020.09.10 |
설정
트랙백
댓글
글
Chernoff bound(체르노프 유계)
체르노프 유계(Chernoff bound)는 마르코프 부등식(Markov's Inequality)과 체비쇼프 부등식(Chebyshyov's Inequality)과 같이 확률분포의 평균만 주어진 경우 또는 평균값과 분산값만 주어졌을때 확률의 상한(Upperbound)을 구할수 있게 하는 것을 목표로 합니다. 다시 말해, 평균이 특정 구간 내에 포함될 확률에 대한 정보를 제공하는 것을 목표로 합니다.
먼저 정의를 보인 후 간단한 증명을 한 다음 예제를 통해 체르노프 유계를 이해해보도록 합시다.
정의
\(X\)가 \(1\leq i\leq n\) 구간에서 \(X_i\in\{0,1\}\)이고 \(P(X_i=1)=p_i\)일 때 \(E[X_i]=p_i\)라고 합시다.
\(X\)가 독립 랜덤변수, 즉 \(X=\sum^n_{i=1}X_i\)일 때 \(\mu\)는 \(X\)의 평균이라 하였을때
$$When\;\delta>0\;\begin{cases}P(X>(1+\delta)\mu) <(\frac{e^\delta}{(1+\delta)^{(1+\delta)}})^{\mu}\\P(X<(1-\delta)\mu) < (\frac{e^{-\delta}}{(1-\delta)^{(1-\delta)}})^\mu\end{cases}$$
이를 그림으로 나타내면 다음과 같습니다.
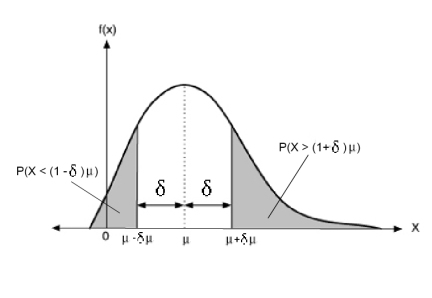
위 그래프를 보면 아시듯이 체르노프 유계는 평균을 중심으로 하여 \(\delta\)만큼 떨어진 구간에서부터 끝부분 까지의 꼬리 분포(Tail distribution)확률을 나타낸 것입니다. 이를 통해 평균을 기준으로 확률의 상한 및 하한을 알 수 있습니다.
지금부터는 체르노프 유계를 증명하고자 합니다. 증명에 어려움을 느끼시는 분이라면 증명 부분을 건너뛰고 응용 사례를 먼저 보고 오시는 것을 추천 드립니다.
증명
먼저 마르코프 부등식(Marcov's Inequality)에 대한 이해가 필요합니다. 여기서는 체르노프 유계를 이해하기 위한 중요한 부분만을 보여드리고자 하오니 마르코프 부등식에 대해 좀 더 자세하게 알아보고자 하시는 분은 아래의 링크를 통해 확인해주시길 바랍니다.
m.blog.naver.com/PostView.nhn?blogId=mykepzzang&logNo=220838855204
[확률과 통계] 28. 마르코프 부등식과 체비쇼프 부등식, Markov's Inequality & Chebyshev's Inequality
이번 포스팅에서는 확률이론에서 유명한 부등식 두 가지를 설명하려 합니다. 우선 첫 번째 '마르코프 부등...
blog.naver.com
마르코프 부등식에서 랜덤 변수 X가 주어졌을 때
$$For\:any\:random\:variable\:X\geq0$$
$$P(X>\lambda)<\frac{E[X]}{\lambda}$$
$$P(f(X)>f(\lambda))<\frac{E[f(X)]}{f(\lambda)}$$
만약 \(f\)가 감소하지 않는 함수일 때 다음과 같은 공식이 성립됩니다.
$$P(X>\lambda)=P(f(X)>f(\lambda))<\frac{E[f(X)]}{f(\lambda)}$$
다음으로 적률생성함수(Moment Generating Function)을 통해 체르노프 유계를 이해해보도록 하겠습니다. 여기서는 체르노프 유계를 증명하기 위한 방법만 소개드리고자 하오니 적률생성함수에 대해 자세히 알고 싶으신 분은 아래의 자료를 참조해주시기 바랍니다.
m.blog.naver.com/mykepzzang/220846464280
[확률과 통계] 45. 적률과 적률생성함수, Moment & Moment-Generating Function
이번 포스팅에서는 '적률생성함수'를 알아보려고 합니다. 적률생성함수는 확률통계학에서 매우 중요하게 다...
blog.naver.com
적률생성함수를 통해 상한값을 구할 때 다음과 같은 식을 유도할 수 있습니다. 만약 확률변수 X가 베르누이 분포라 가정하였을 때 다음과 같은 식을 유도할 수 있습니다.
$$\begin{split}
E[e^{tX}]&= E[e^{t\sum X_{i}}] \\
&=\sum^n_{x=0}e^{tx}\left(\begin{array}{c}n\\ x\end{array}\right)p^x(1-p)^{n-x}\\
&=\sum^n_{x=0}\left(\begin{array}{c}n\\x\end{array}\right)(pe^t)^x(1-p)^{n-x}\\
&\leq\prod_ie^{p_i(e^t-1)}\\
&=e^{\sum_ip_i(e^t-1)}\\
&=e^{(e^t-1)\mu}
\end{split}$$
※증명
이제 본격적으로 체르노프 유계를 증명해보도록 하겠습니다. 위에서 보여드렸던 마르코프 부등식에 \(\lambda\)를 \((1+\delta)\mu\)로 대입하면 다음과 같은 식이 구해집니다.
$$\begin{split}
P(X>(1+\delta)\mu)&=P(e^{tX}>e^{t(1+\delta)\mu})\\
&\leq\frac{E[e^{tX}]}{e^{t(1+\delta)\mu}}\\
&\leq\frac{e^{(e^t-1)\mu}}{e^{t(1+\delta)\mu}}
\end{split}$$
위의 식을 최소화시키기 위해 t에 다음과 같은 값을 대입합니다.
$$t=ln(1+\delta)$$
이를 식에 넣어 정리하면 다음과 같습니다.
$$\begin{split}
P(X>(1+\delta)\mu)
&\leq\frac{e^{(e^{ln(1+\delta)}-1)\mu}}{e^{(1+\delta)ln(1+\delta)\mu}}\\
&=\left(\frac{e^{(e^{ln(1+\delta)}-1)}}{e^{(1+\delta)ln(1+\delta)}}\right)^\mu\\
&=\left(\frac{e^\delta}{(1+\delta)^{1+\delta}}\right)^\mu
\end{split}$$
위 식을 통해 체르노프 유계의 한쪽 끝부분인 상한을 증명하였습니다. 하한 또한 위의 식으로 갈음할 수 있으므로 주어진 체르노프 유계의 정의는 증명되었음을 확인하였습니다.
응용
지금까지 체르노프 유계의 정의와 증명과정을 살펴보았습니다. 이번에는 체르노프 유계가 어떻게 적용될 수 있는지 살펴보도록 하겠습니다.
아래의 그림은 하나의 집단에서 야구와 축구를 좋아하는 사람들을 나타낸 것입니다.

위 집단에서 좋아하는 운동에 대해 물어보았을 때 축구를 좋아할 확률을 \(p\)라고 하였을 때, 몇명이 축구를 좋아할까요?
그림상으로는 총 인원수가 적기 때문에 금방 알아낼 수 있지만 만약 1만명 이상의 인원을 대상으로 한 사람씩 물어보는 것은 상당히 많은 시간이 소요되기 때문에 사실상 불가능합니다.
최대한 균등하고 독립적으로 임의의 표본으로 n명을 뽑은 다음 \(X=\widetilde{p}n\)으로 계산하여 축구를 좋아하는 인원수를 구할 수 있을 것입니다. 즉, \(\widetilde{p}=\frac{X}{n}\)을 통해 확률 \(p\)를 예측할 수 있을 것으로 기대됩니다.
X가 이항 랜덤 변수로 n회의 베르누이 수행을 하였고 성공확률이 p라고 예상하였을 때 모집단이 표본집단의 크기 n보다 충분히 클 때 다음이 성립됨을 알 수 있습니다.
$$E[X]=np$$
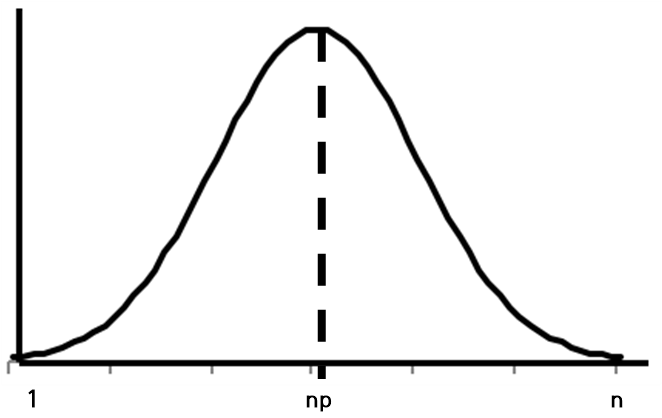
다음과 같이 분포에서 평균 np의 위치를 쉽게 알 수 있습니다. 그렇다면 우리가 예상한 \(p\)가 실제 확률 \(\tilde{p}\)에 얼마나 근접한지 알 수 있을까요?
\(p\)의 신뢰구간 \(1-\gamma\)을 \([\widetilde{p}-\delta,\tilde{p}+\delta]\)라 하였을 때 \(\gamma>0,\:\delta>0\)의 조건에서 다음과 같이 나타낼 수 있습니다.
$$P(p\in[\tilde{p}-\delta,\tilde{p}+\delta])\geq1-\gamma$$
즉 위의 식을 \(\gamma\)에 대해 다음과 같이 나타낼 수 있습니다.
$$P(p<\tilde{p}-\delta)+P(p>\tilde{p}+\delta)<\gamma$$
이번에는 위에서 정의한 \(\gamma\)값에 대해 알아보도록 하겠습니다. 먼저 하한 구간에 대해 다음과 같이 구할 수 있습니다.
$$\begin{split}
P(p<\tilde{p}-\delta) &= P(\tilde{p}>p+\delta)\\
&= P(X>n(p+\delta)) \\
&= P(X>E[X](1+\frac{\delta}{p}))\\
&< e^{-\frac{np(\frac{\delta}{p})^2}{3}}\\
&= e^{-\frac{n\delta^2}{3p}}\\
&\leq e^{-\frac{n\delta^2}{3}}
\end{split}$$
다음으로 상한 구간에 대해 다음과 같이 구할 수 있습니다.
\begin{split}
P(p>\tilde{p}+\delta) &= P(\tilde{p}<p-\delta)\\
&= P(X<n(p-\delta)) \\
&= P(X<E[X](1-\frac{\delta}{p}))\\
&< e^{-\frac{np(\frac{\delta}{p})^2}{2}}\\
&= e^{-\frac{n\delta^2}{2p}}\\
&\leq e^{-\frac{n\delta^2}{2}}
\end{split}
위의 식을 통해 우리는 \(\gamma\)값을 다음과 같이 알아낼 수 있습니다.
$$\gamma=e^{-\frac{n\delta^2}{2}}+e^{-\frac{n\delta^2}{3}}$$
위의 식을 보았을 때 갑자기 자연상수 e의 지수의 분모가 뜬금없이 2 혹은 3이 되어있는 것을 확인하실 수 있습니다. 앞에서 말씀드렸듯이 \(\delta\)는 매우 작은 값이고 위의 부등식을 통해 2 혹은 3을 대입하였을 때 \(\gamma\)의 값이 약간 넓어지면서 예측값 p의 범위가 더욱 타이트해졌음을 보실 수 있습니다. 즉, 편의상 간단하게 2 혹은 3을 대입하여 범위를 한정시킬 수 있어 2 혹은 3으로 대체해도 무방하다는 의미입니다.
즉, 예측값 p를 구하기 위해 우리는 \(\gamma\), \(\delta\)와 n의 값을 조절함으로서 신뢰구간을 조정하여 범위를 한정함으로서 궁극적인 목표인 평균의 특정 구간을 한정함으로서 원하는 결과를 얻을 수 있음을 확인할 수 있습니다.
'공대생의 팁' 카테고리의 다른 글
| MobaXterm에서 X server 사용시 전체화면 모드 화면이 안나올때 해결방법 (1) | 2020.10.25 |
|---|---|
| 여분기여도(Marginal Contribution) (0) | 2020.09.13 |
| wget 사용시 증명서(certificate) 관련 문제가 발생하였을 때 해결방법 (0) | 2020.09.11 |
| WSL(Windows Subsystem for Linux )에서 'Can't open display: :0.0' 오류 발생시 해결방법 (1) | 2020.09.10 |
| 모션 증폭(Motion Magnification) (0) | 2020.08.15 |

