검색결과 리스트
글
Gower's distance(가워 거리)
인간의 경험에 있어서 거리의 개념은 직관적으로 예상할 수 있습니다. 측정기준이라는 용어는 종종 측정을 위한 표준으로 사용되는 반면, 일상 생활에서는 일반적으로 두 지점의 물리적인 가까움 또는 아이디어 사이가 어느 정도 되는지의 근접성을 의미합니다. 관측치 사이의 거리 또는 정량적 또는 정성적 변수 사이의 거리를 고려할 수도 있습니다.
데이터를 클러스터링하는 동안 가장 중요한 작업 중 하나는 각 데이터 포인트 사이의 거리를 계산하는 데 사용할 방법을 결정하는 것입니다. 생물학, 사회과학 또는 마케팅 조사와 같이 클러스터 분석이 일반적으로 사용되는 다양한 실제 분야에서는 수치 변수와 카테고리 변수를 모두 갖는 데이터셋이 적용되는 경우가 많습니다. 이러한 유형의 데이터를 혼합 데이터(Mixed data)라고 합니다. 많은 거리 측정방법이 존재하며, 그 중 여기서 소개해드리고자 하는 것은 데이터가 혼합 데이터일 때 사용되는 가워 거리(Gower's distance - 1971)입니다.
가워 거리(Gower's distance)란 무엇인가?
가워 거리(Gower's Distance)는 가워 차이 계수(Gower's dissimilarity coefficient)라고도 하며 사용하여 두 데이터의 차이를 측정할 수 있습니다. 기록에는 논리, 카테고리, 수치 또는 텍스트 데이터의 조합이 포함될 수 있습니다. 거리는 항상 0(동일함)에서 1(가장 큰 차이) 사이의 숫자입니다.
q개의 차원을 가지고 있는 벡터 \(\textbf{x}\)가 있다고 하였을 때 \(\textbf{x}\)가 p개의 카테고리형 변수를 갖고 있다 하였을 때
$$\LARGE{\textbf{x} = (x_1, x_2, ... , x_p, x_{p+1}, ..., x_q)}$$
위 벡터에서 p개의 카테고리형 변수의 q-p개의 수치형 변수가 있다고 하였을 때 해당 식을 아래와 같이 다시 쓸 수 있습니다.
$$\LARGE{\textbf{x} = (z_1, ..., z_p, c_1, ..., c_{q-p})^\top=(\textbf{z}^\top,\textbf{c}^\top)}$$
여기서 벡터 \(\textbf{z}^\top\)와 \(\textbf{c}^\top\)는 벡터 \(\textbf{x}\)의 부분집합입니다. 이 때 두 데이터 포인트 \(\textbf{x}_i=(\textbf{z}_i^\top,\textbf{c}_i^\top)\) 와 \(\textbf{x}_j=(\textbf{z}_j^\top,\textbf{c}_j^\top)\)의 가워 거리 \(D_{x_ix_j}\)를 구하는 식은 다음과 같이 나타낼 수 있습니다.
$$\LARGE{D_{x_{i}x_{j}}=\dfrac{\sum^{p}_{r=1}W_{x_{i}x_{j}z_{r}}D_{x_{i}x_{j}z_{r}}}{\sum^{p}_{r=1}W_{x_{i}x_{j}z_{r}}}+\dfrac{\sum^{q-p}_{r=1}W_{x_{i}x_{j}c_{r}}D_{x_{i}x_{j}c_{r}}}{\sum^{q-p}_{r=1}W_{x_{i}x_{j}c_{r}}}}$$
여기서 \(W_{x_{i}x_{j}z_{r}}\) 와 \(W_{x_{i}x_{j}c_{r}}\) 는 각각 카테고리형 변수 \(z_r\)과 수치형 변수 \(c_r\)에 해당되는 가중치값을 나타냅니다.
\(D_{x_{i}x_{j}z_{r}}\) 카테고리형 변수의 \(z_r\)의 거리를 나타낸 것으로 다음과 같은 식으로 나타냅니다.
$$\LARGE{D_{x_{i}x_{j}z_{r}}=\begin{cases}0,\quad z_{r}^{i}=z_{r}^{j}\\1,\quad otherwize\end{cases}}$$
만약 두 카테고리형 변수가 같은 값일 경우 0, 다른 값일 경우 1이 된다고 이해하면 쉬울 것입니다.
\(D_{x_{i}x_{j}c_{r}}\)은 실수인 수치형 변수로서 우리가 흔히 아는 맨허튼 거리(\(L_1\) norm) 방식으로 값을 구합니다.
$$\LARGE{D_{x_ix_jc_r}=\dfrac{|c_r^i-c_r^j|}{\max(c_r)-\min(c_r)}}$$
위 식을 보았을 때, 각 변수의 차의 절대값에 실수 \(c\)의 범위(최대값 - 최소값)을 나눔으로서 변수의 거리를 알 수 있습니다. 여기서는 맨허튼 거리를 예제로 하였지만 좀 더 좋은 공식이 있다면 그것을 사용해도 무방합니다.
예제
다음과 같은 데이터가 있다고 합시다.
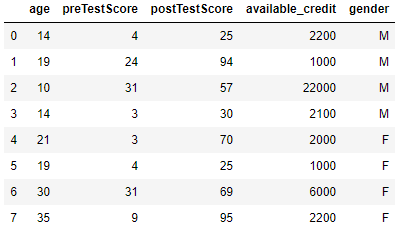
위 데이터를 보았을 때 [age, perTestScore, postTestScore, available_credit] 4개의 변수는 수치형 변수이고 [gender] 1개의 변수는 카테고리형 변수임을 알 수 있습니다. 즉 이를 벡터로 나타내면 다음과 같습니다.
$$\LARGE{\textbf{x} = (c_1, c_2, c_3, c_4, z_1)}$$
이 때 weight를 1이라고 하였을 때 가워 거리는 다음과 같이 나타낼 수 있습니다.
$${D_{x_ix_j}=\dfrac{|c_1^i-c_1^j|}{\max(c_1)-\min(c_1)}+\dfrac{|c_2^i-c_2^j|}{\max(c_2)-\min(c_2)}+\dfrac{|c_3^i-c_3^j|}{\max(c_3)-\min(c_3)}+\dfrac{|c_4^i-c_4^j|}{\max(c_4)-\min(c_4)}+D_{x_{i}x_{j}z_{1}}}$$
주어진 벡터에서 \(x_0\)을 기준으로 각 row별로 가워 거리를 구하면 다음과 같습니다.
$$D_{x_{0}x_{1}}=\dfrac{\left|14-19\right|}{35-10}+\dfrac{\left|4-24\right|}{31-3}+\dfrac{\left|25-94\right|}{95-25}+\dfrac{\left|2200-1000\right|}{22000-1000}+0 \\ = 1.9572$$
$$D_{x_{0}x_{2}}=\dfrac{\left|14-10\right|}{35-10}+\dfrac{\left|4-31\right|}{31-3}+\dfrac{\left|25-57\right|}{95-25}+\dfrac{\left|2200-22000\right|}{22000-1000}+0 \\ = 0.2529$$
$$D_{x_{0}x_{3}}=\dfrac{\left|14-14\right|}{35-10}+\dfrac{\left|4-3\right|}{31-3}+\dfrac{\left|25-30\right|}{95-25}+\dfrac{\left|2200-2100\right|}{22000-1000}+0 \\ = 0.1120$$
$$D_{x_{0}x_{4}}=\dfrac{\left|14-21\right|}{35-10}+\dfrac{\left|4-3\right|}{31-3}+\dfrac{\left|25-70\right|}{95-25}+\dfrac{\left|2200-2000\right|}{22000-1000}+1 \\ = 1.9681$$
$$D_{x_{0}x_{5}}=\dfrac{\left|14-19\right|}{35-10}+\dfrac{\left|4-4\right|}{31-3}+\dfrac{\left|25-25\right|}{95-25}+\dfrac{\left|2200-1000\right|}{22000-1000}+1 \\ = 1.2571$$
$$D_{x_{0}x_{6}}=\dfrac{\left|14-30\right|}{35-10}+\dfrac{\left|4-31\right|}{31-3}+\dfrac{\left|25-69\right|}{95-25}+\dfrac{\left|2200-6000\right|}{22000-1000}+1 \\ = 3.4138$$
$$D_{x_{0}x_{7}}=\dfrac{\left|14-35\right|}{35-10}+\dfrac{\left|4-9\right|}{31-3}+\dfrac{\left|25-95\right|}{95-25}+\dfrac{\left|2200-2200\right|}{22000-1000}+1 \\ = 3.0186$$
위 계산을 보았을 때 \(x_0\)에서 Gower's distance가 가장 가까운 것은 \(x_3\)이고 가장 먼 것은 \(x_6\)임을 알 수 있습니다.
- 참고자료
https://medium.com/analytics-vidhya/gowers-distance-899f9c4bd553
Gower’s Distance
One of the most important task while clustering the data is to decide what metric to be used for calculating distance between each data ….
medium.com
https://jamesmccaffrey.wordpress.com/2020/04/21/example-of-calculating-the-gower-distance/
Example of Calculating the Gower Distance
The Gower distance is a metric that measures the dissimilarity of two items with mixed numeric and non-numeric data. Gower distance is also called Gower dissimilarity. One possible use of Gower dis…
jamesmccaffrey.wordpress.com
Gower Distance
Tuerhong, G., & Kim, S. B. (2014). Gower distance-based multivariate control charts for a ...
blog.naver.com
'공대생의 팁' 카테고리의 다른 글
| python에서 pip install 과정에서 SSL 오류 해결방법 (0) | 2021.03.16 |
|---|---|
| USB없이 GRUB2를 통해 ISO파일 부팅하기(DVD 없이 우분투 설치) (0) | 2021.03.11 |
| 2021년 이후 어도비 플래시 플레이어를 사용하는 방법 (4) | 2021.01.16 |
| MobaXterm에서 X server 사용시 전체화면 모드 화면이 안나올때 해결방법 (1) | 2020.10.25 |
| 여분기여도(Marginal Contribution) (0) | 2020.09.13 |
